
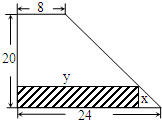
 某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )
某厂有许多形状为直角梯形的铁皮边角料,如图,为降低消耗,现要从这些边角料上截取矩形铁片(图中阴影部分)备用,当截取的矩形面积最大时,矩形的两边长x、y应为( )| A. | x=15,y=12 | B. | x=12,y=15 | C. | x=14,y=10 | D. | x=10,y=14 |
分析 作DH⊥BC于H,如图,则BH=AD=8,CH=BC-BH=16,DH=AB=20,BE=y,EF=x,先证明△CEF∽△CHD,利用相似比可得y=-$\frac{4}{5}$x+24,则根据矩形面积公式得到矩形BEFG的面积=-$\frac{4}{5}$x2+24x,然后根据二次函数的最值问题求解.
解答 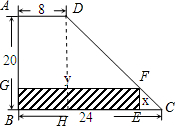 解:作DH⊥BC于H,如图,则BH=AD=8,CH=BC-BH=16,DH=AB=20,BE=y,EF=x,
解:作DH⊥BC于H,如图,则BH=AD=8,CH=BC-BH=16,DH=AB=20,BE=y,EF=x,
∵EF∥DH,
∴△CEF∽△CHD,
∴$\frac{CE}{CH}$=$\frac{EF}{DH}$,即$\frac{24-y}{16}$=$\frac{x}{20}$,
∴y=-$\frac{4}{5}$x+24,
∴矩形BEFG的面积=xy=x•(-$\frac{4}{5}$x+24)
=-$\frac{4}{5}$x2+24x,
当x=-$\frac{24}{2×(-\frac{4}{5})}$=15时,矩形BEFG的面积最大,此时y=-$\frac{4}{5}$×15=24=12.
故选A.
点评 本题考查了相似三角形的应用:先画出几何图形,再通过证明三角形相似计算出相应线段的长和线段之间的关系,然后解决问题.也考查了直角梯形的性质和二次函数的最值问题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $y=[{\frac{x+1}{10}}]$ | B. | $y=[{\frac{x+2}{10}}]$ | C. | $y=[{\frac{x+3}{10}}]$ | D. | $y=[{\frac{x+4}{10}}]$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-a+b}{a-b}$=-1 | B. | $\frac{{a}^{2}+{b}^{2}}{a+b}$=a+b | C. | $\frac{2a-b}{2a+b}$=$\frac{a-b}{a+b}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a+b}$=a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com