
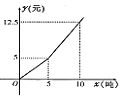
【题目】为了鼓励市民节约用水,自来水公司特制定了新的用水收费标准,每月用水量,x(吨)与应付水费(元)的函数关系如图.
(1)求出当月用水量不超过5吨时,y与x之间的函数关系式;
(2)某居民某月用水量为8吨,求应付的水费是多少?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ![]() -1;
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 的图象
的图象![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.
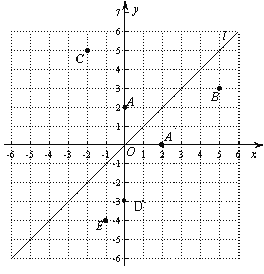
实验与探究:由图观察易知A(0,2)关于直线![]() 的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线
的对称点A′的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线![]() 的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
的对称点B′、C′的位置,并写出它们的坐标: B′____________、C′___________;
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为____________;
的坐标为____________;
运用与拓广:已知两点D(0,-3)、E(-1,-4),试在直线![]() 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
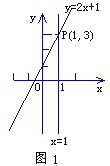
【题目】阅读,我们知道,在数轴上,x=1表示一个点,而在平面坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形,就是一次函数y=2x+1的图象,它也是一条直线,如图1,可以得出,直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为![]()
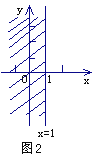
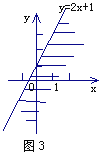
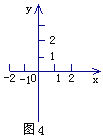
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧的部分,如图2;y≤2x+1,也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3.
回答下列问题:
(1)在直角坐标系(如图4)中,用作图的方法求方程组![]() 的解;
的解;
(2)用阴影表示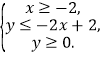 所围成的区域.
所围成的区域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题: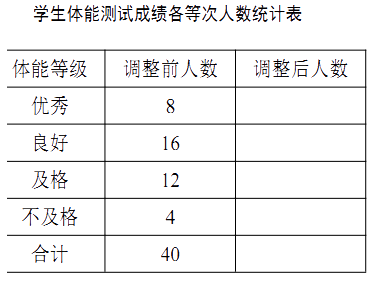
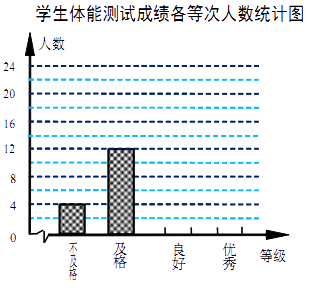
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第一个正方形的顶点A1(﹣1,1),B1(1,1);第二个正方形的顶点A2(﹣3,3),B2(3,3);第三个正方形的顶点A3(﹣6,6),B3(6,6)按顺序取点A1,B2,A3,B4,A5,B6…,则第12个点应取点B12,其坐标为( )

A. (12,12) B. (78,78) C. (66,66) D. (55,55)
查看答案和解析>>
科目:初中数学 来源: 题型:
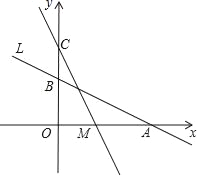
【题目】如图,直线L:y=-![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com