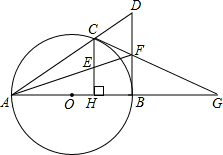
(1)证明:∵BD是⊙O的切线,∴∠DBA=90°。
∵CH⊥AB,∴CH∥BD。∴△AEC∽△AFD。
∴

。∴AE•FD=AF•EC。
(2)证明:∵CH∥BD,∴△AEC∽△AFD,△AHE∽△ABF。∴

。
∵CE=EH(E为CH中点),∴BF=DF。
∵AB为⊙O的直径,∴∠ACB=∠DCB=90°。∴CF=DF=BF,即CF=BF。
(3)解:∵BF=CF=DF(已证),EF=BF=2,∴EF=FC。∴∠FCE=∠FEC。
∵∠AHE=∠CHG=90°,∴∠FAH+∠AEH=90°,∠G+∠GCH=90°。
∵∠AEH=∠CEF,∴∠G=∠FAG。∴AF=FG。
∵FB⊥AG,∴AB=BG。
连接OC,BC,
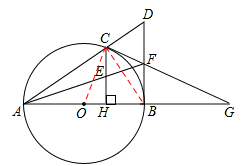
∵BF切⊙O于B,∴∠FBC=∠CAB。
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC
∴∠FCB=∠CAB。
∵∠ACB=90°,∴∠ACO+∠BCO=90°。∴∠FCB+∠BCO=90°,即OC⊥CG。
∴CG是⊙O切线。
∵GBA是⊙O割线,FB=FE=2,由切割线定理得:(2+FG)
2=BG×AG=2BG
2,
【注,没学切割线定理的可由△AGC∽△CGB求得】
在Rt△BFG中,由勾股定理得:BG
2=FG
2﹣BF
2,∴FG
2﹣4FG﹣12=0。
解得:FG=6,FG=﹣2(舍去)。
由勾股定理得:AB=BG=

。
∴⊙O的半径r是

。

 。∴AE•FD=AF•EC。
。∴AE•FD=AF•EC。 。
。
 。
。 。
。

 阅读快车系列答案
阅读快车系列答案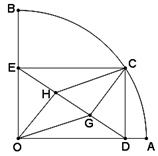
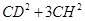 是定值.
是定值.