
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计(满分100分,学生成绩取整数),并按照成绩从低到高分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个小组,绘制统计图如下(未完成),解答下列问题:
五个小组,绘制统计图如下(未完成),解答下列问题:

(1)样本容量为______,频数分布直方图中![]() ______;
______;
(2)扇形统计图中![]() 小组所对应的扇形圆心角为______度,并补全频数分布直方图;
小组所对应的扇形圆心角为______度,并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
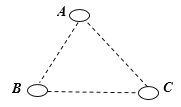
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的茶文化源远流长,根据制作方法和茶多酚氧化(发酵)程度的不同,可分为六大类:绿茶(不发酵)、白茶(轻微发酵)、黄茶(轻发酵)、青茶(半发酵)、黑茶(后发酵)、红茶(全发酵).春节将至,为款待亲朋好友,小叶去茶庄选购茶叶.茶庄有碧螺春、龙井两种绿茶,一种青茶——武夷岩茶及一种黄茶——银针出售.
(1)随机购买一种茶叶,是绿茶的概率为________;
(2)随机购买两种茶叶,求一种是绿茶、一种是银针的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测、距某城市![]() 的正南方向
的正南方向![]() 千米
千米![]() 处有一台风中心,其中心最大风力为
处有一台风中心,其中心最大风力为![]() 级,每远离台风中心
级,每远离台风中心![]() 千米风力就会减弱一级,该台风中心现正以
千米风力就会减弱一级,该台风中心现正以![]() 千米/时的速度沿北偏东
千米/时的速度沿北偏东![]() 方向往
方向往![]() 移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响
移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称为受台风影响
![]() 该城市是否会受到这交台风的影响?请说明理由;
该城市是否会受到这交台风的影响?请说明理由;
![]() 若会受到台风影响,那么台风影响该城市持续时间有多少?
若会受到台风影响,那么台风影响该城市持续时间有多少?
![]() 该城市受到台风影响的最大风力为几级?
该城市受到台风影响的最大风力为几级?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A是双曲线![]() 在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。
在第一象限的分支上的一个动点,连接AO并延长与这个双曲线的另一分支交于点B,以AB为底边作等腰直角三角形ABC,使得点C位于第四象限。
(1)点C与原点O的最短距离是________;
(2)没点C的坐标为(![]()
![]() ,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。
,点A在运动的过程中,y随x的变化而变化,y关于x的函数关系式为________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.
(1)求经过几秒钟M、N两点停止运动?
(2)求点A、E、M、N构成平行四边形时,M、N两点运动的时间;
(3)设运动时间为t(s),用含字母t的代数式表示△EMN的面积S(cm2).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的。
是“中心轴对称”的。
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的。
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,![]() 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com