
【题目】如图,抛物线 y ax2 2a(x a<0)位于 x 轴上方的图象记为F1,它与 x 轴交于 P1、O 两点,图象 F2与F1关于原点 O 对称, F2 与 x 轴的另一个交点为 P2 , F1 将与 F2 同时沿 x 轴向右平移 P1 P2 的长度即可得到F3与F4 ;再将 F3与F4 同时沿 x 轴向右平移 P1 P2 的长度即可得到 F5与F6 ;…;按这样的方式一直平移下去即可得到一系列图象 F1,F2,,Fn .我们把这组图象称为“波浪抛物线”.
(1)当 a=﹣1 时,
①求 F1 图象的顶点坐标;
②点 H(2014,﹣3) (填“在”或“不在”)该“波浪抛物线”上;若图象 F n的顶点 T n的横坐标为201,则图象 F n对应的解析式为 , 其自变量 x 的取值范围为 .
(2)设图象 Fn、Fn+1 的顶点分别为 Tn、Tn+1 (n 为正整数),x 轴上一点 Q 的坐标为(12,0).试探究: 当 a 为何值时,以 O、 Tn、Tn+1 、Q 四点为顶点的四边形为矩形?并直接写出此时 n 的值.

【答案】(1)①(﹣1,1);②不在, y =(x﹣201)2﹣1 ,200≤x≤202;(2)a=﹣![]() ,故此时 n 的值为 4.
,故此时 n 的值为 4.
【解析】
(1)①a=-1代入抛物线的解析式,然后令y=可求得对应的x的值,从而可得到p1的坐标,然后依据平移的方向和距离可得到点P2的坐标,接下来,利用配方法可求得抛物线的顶点F1的坐标②根据该“波浪抛物线”顶点坐标纵坐标分别为1和-1即可得出结论;
(2)设OQ中点为O′,则线段TnTn+1经过O′,再根据图形平移的性质即可得出结论.
(1)①当a=-1时,y=ax2+2ax=-x2-2x.
令-x2-2x=0,解得:x=0或x=-2.
∴点P1的坐标为(-2,0).
由平移的性质可知P2的坐标为(2,0).
∵y=-x2-2x=(x+1)2+1,
∴图象F1的顶点坐标为:(-1,1);
②∵该“波浪抛物线”顶点坐标纵坐标分别为1和-1,
∴点H(2015,-2),不在该“波浪抛物线”上,
∵图象Fn的顶点Tn的横坐标为201,
201÷4=50…1,故其图象与F2,F4…形状相同,
则图象Fn对应的解析式为:y=(x-201)2-1,
其自变量x的取值范围为:200≤x≤202.
(2)设OQ中点为O′,则线段TnTn+1经过O′,
由题意可知OO′=O′Q,O′Tn=O′Tn+1,
∴当TnTn+1=OQ=12时,四边形OTnTn+1Q为矩形,
∴O′Tn+1=6,
∵F1对应的解析式为y=a(x+1)2-a,
∴F1的顶点坐标为(-1,-a),
∴由平移的性质可知,点Tn+1的纵坐标为-a,
∴由勾股定理得(-a)2+(-1)2=62,
∴a=±![]() ,
,
∵a<0,
∴a=﹣![]() ,故此时 n 的值为 4.
,故此时 n 的值为 4.


科目:初中数学 来源: 题型:
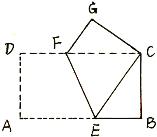
【题目】如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)试判断△CEF的形状,并证明你的结论;
(3)若AB=8,AD=4,求四边形ECGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=25°,O为AB的中点. 将OA绕点O逆时针旋转θ °至OP(0<θ<180),当△BCP恰为轴对称图形时,θ的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为养成学生课外阅读的习惯,各学校普遍开展了“我的梦.中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
(1)表中 a= ,b= ;
(2)请补全频数分布直方图中空缺的部分;
(3)样本中,学生日阅读所用时间的中位数落在第 组;
(4)请估计该校七年级学生日阅读量不足 1 小时的人数.
组别 | 时间段(小时) | 频数 | 频率 |
1 | 0≤x<0.5 | 10 | 0.05 |
2 | 0.5≤x<1.0 | 20 | 0.10 |
3 | 1.0≤x<1.5 | 80 | b |
4 | 1.5≤x<2.0 | a | 0.35 |
5 | 2.0≤x<2.5 | 12 | 0.06 |
6 | 2.5≤x<3.0 | 8 | 0.04 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,点O是BC的中点,如果点M、N分别在线段AB、AC上移动,并在移动过程中始终保持AN=BM.
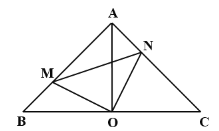
(1)求证:△ANO≌△BMO;
(2)求证:OM⊥ON.
查看答案和解析>>
科目:初中数学 来源: 题型:
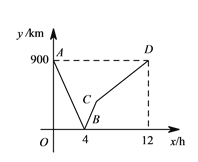
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,根据图象进行一下探究:
之间的函数关系,根据图象进行一下探究:
信息读取(1)甲、乙两地之间的距离为______![]() :
:
(2)请解释图中点![]() 的实际意义:_______
的实际意义:_______
图象理解(3)求慢车和快车的速度:
(4)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围:
的取值范围:
问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇![]() 分钟后,第二列快车与慢车相遇,求第二列快车比第一列快车晚出发多少小时?
分钟后,第二列快车与慢车相遇,求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
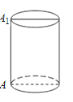
【题目】如图,有一木质圆柱笔筒的高为9cm,底面半径为2cm,现要围绕笔筒的表面由A到A1(A,A1在圆柱的同一轴截面上)镶上一条银色金属线作为装饰,则这条金属线的最短长度是_________cm.(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
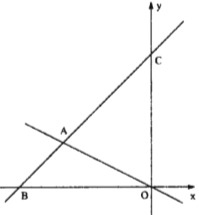
【题目】如图,平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求直线![]() 的表达式.
的表达式.
(2)求![]() 的面积.
的面积.
(3)直接写出使![]() 的面积是
的面积是![]() 面积的
面积的![]() 的点
的点![]() 坐标.
坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com