小华看到了坐标系中点A关于y轴的对称点为B(a,b),而点B关于x轴的对称点为C(-3,-2),点A关于x轴对称点为D,若将A、B、C、D各点的纵坐标加3后描出变化后的A、B、C、D各点,并顺次连接,求出此四边形面积.
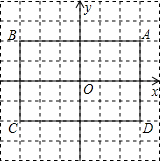
解:∵B关于x轴的对称点为C(-3,-2),
∴B(-3,2),
∵点A关于y轴对称点为B(-3,2),
∴A(3,2),
∵点A关于x轴对称点为D,
∴D点坐标为(3,-2).
∴△ABCD的面积为:AD•DB=4×6=24.
分析:首先根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数得到B点坐标,再根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变得到A点坐标,再求出D点坐标,然后利用坐标系画出图形,即可求出答案.
点评:此题主要考查了关于x轴、y轴对称的点的坐标及矩形的面积,根据关于x轴、y轴对称的点的坐标求出A、C、D的坐标是解题的关键.
