
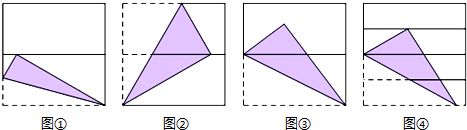
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 如图②,首先运用翻折变换的性质、平行线的性质证明∠FBE=∠EBG(设为α),此为解题的关键性结论;再次证明∠ABD=∠FBE=α,求出α=30°;
如图④,首先运用翻折变换的性质证明∠MAB=60°,求出∠BAC=60°,进而得到∠ACB=,30°,即可解决问题.
解答  解:如图②,由题意得:AD∥CF,AC=BC
解:如图②,由题意得:AD∥CF,AC=BC
∴DF=BF,EF为直角△BDE斜边上的中线,
∴EF=BF,∠FBE=
∠FEB;而EF∥BC,
∴∠FEB=∠EBG,∠FBE=∠EBG(设为α);
由题意得:∠ABD=∠FBE=α,而∠ABG=90°,
∴3α=90°,α=30°;
如图④,由题意得:AN=AB=2AM,∠AMB=90°,
∴∠ABM=30°,∠MAB=60°;
由题意得:∠NAC=∠BAC=$\frac{180°-60°}{2}$=60°,
∴∠ACB=90°-60°=30°,
综上所述,有一个锐角为30°的直角三角形有两个,
故选C.
点评 该题以正方形为载体,主要考查了翻折变换的性质、直角三角形的性质等几何知识点及其应用问题;牢固掌握翻折变换的性质、直角三角形的性质等几何知识点是解题的基础和关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
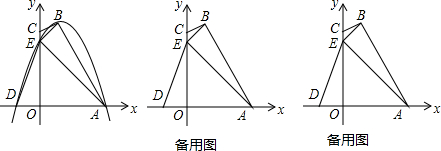
 以点A(0,2),B(4,2),C(0,4)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.
以点A(0,2),B(4,2),C(0,4)为顶点的四边形OABC在平面直角坐标系中位置如图,现将四边形OABC沿直线AC折叠使点B落在点D处,AD交OC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
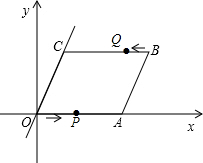 如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)
如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com