
 �Ķ����ϣ�������⣮
�Ķ����ϣ�������⣮���� ��1�����ݺ���ͼ��д����������x���·����ֵ�x��ȡֵ��Χ���ɣ�
��2����a��0��a=0��a��0�����������ͼ�Σ�Ȼ��д����������x���Ϸ����ֵ�x��ȡֵ��Χ���ɣ�
��3����a��2��a=2��0��a��2��a��0�����������ͼ�Σ�Ȼ��д����������x���Ϸ����ֵ�x��ȡֵ��Χ���ɣ�
��� �⣺��1��-1��x��3��
��2����ͼ��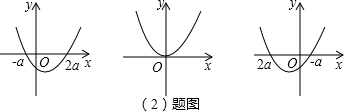
��a��0ʱ��x��2a��x��-a��
��a=0ʱ��x��0��
��a��0ʱ��x��-a��x��2a��
��3����ͼ��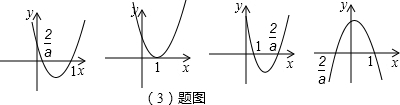
��$a��2ʱ��x��1��x��\frac{2}{a}$��
��a=2ʱ��x��1��
��$0��a��2ʱ��x��\frac{2}{a}��x��1$��
��$a��0ʱ��\frac{2}{a}��x��1$��
���� ���⿼���˶��κ����벻��ʽ��������Ŀ��ȷ��������ͼ���������ν�ϵ�˼�������Ӽ�㣮


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
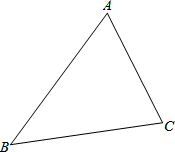 ��һ��סլС�����һ���������̵أ����������н�һ��Բ�λ�̳��ʹ��������������ͼ�л������Բ�λ�̳��λ�ã�
��һ��סլС�����һ���������̵أ����������н�һ��Բ�λ�̳��ʹ��������������ͼ�л������Բ�λ�̳��λ�ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
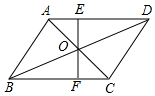 ��֪����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��ֱ��EF�ֱ�AD��E��BC��F��S��AOE=3��S��BOF=5����?ABCD�������32��
��֪����?ABCD�У��Խ���AC��BD�ཻ�ڵ�O������O��ֱ��EF�ֱ�AD��E��BC��F��S��AOE=3��S��BOF=5����?ABCD�������32���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com