
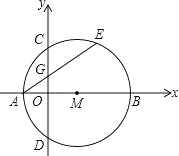
【题目】如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(﹣2,0),AE=8,
(1)求证:AE=CD;
(2)求点C坐标和⊙M直径AB的长;
(3)求OG的长.
【答案】(1)证明见解析(2)(0,4),10(3)![]()
【解析】
试题分析:(1)要证明AE=CD,即证明![]() ,由点C是
,由点C是![]() 的中点和AB⊥CD可知,
的中点和AB⊥CD可知,![]() ,从而可得
,从而可得![]() ;
;
(2)由垂径定理可知:OC=![]() CD=
CD=![]() AE=4,所以点C的坐标为(0,4),连接AC和BC后,证明△CAO∽△BAC,可得CA2=AOAB,从而可求出AB的长度;
AE=4,所以点C的坐标为(0,4),连接AC和BC后,证明△CAO∽△BAC,可得CA2=AOAB,从而可求出AB的长度;
(3)由![]() 可知,AG=CG,设AG=x,则OG=4﹣x,利用勾股定理可列出方程即可求出x的值.
可知,AG=CG,设AG=x,则OG=4﹣x,利用勾股定理可列出方程即可求出x的值.
试题解析:(1)∵点C是![]() 的中点,
的中点,
∴![]() ,
,
∵AB⊥CD,
∴由垂径定理可知:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AE=CD;
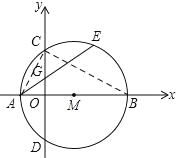
(2)连接AC、BC,
由(1)可知:CD=AE=8,
∴由垂径定理可知:OC=![]() CD=4,
CD=4,
∴C的坐标为(0,4),
由勾股定理可求得:CA2=22+42=20,
∵AB是⊙M的直径,
∴∠ACB=90°,
∵∠CAB=∠CAB,
∴△CAO∽△BAC,
∴![]() ,
,
∴CA2=AOAB,
∴AB=![]() =10;
=10;
(3)由(1)可知:![]() ,
,
∴∠ACD=∠CAE,
∴AG=CG,
设AG=x,
∴CG=x,OG=OC﹣CG=4﹣x,
∴由勾股定理可求得:AO2+OG2=AG2,
∴22+(4﹣x)2=x2,
∴x=![]() ,
,
∴OG=4﹣x=![]()


科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题:
定义:线段AD把等腰三角形ABC分成△ABD与△ACD(如图1),如果△ABD与△ACD均为等腰三角形,那么线段AD叫做△ABC的完美分割线.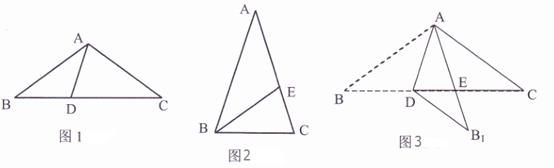
(1)如图1,已知△ABC中,AB=AC,∠BAC=108°,AD为△ABC的完美分割线,且BD<CD,则∠B= , ∠ADC=.
(2)如图2,已知△ABC中,AB=AC,∠A=36°,BE为△ABC的角平分线,求证:BE为△ABC完美分割线.
(3)如图3,已知△ABC是一等腰三角形纸片,AB=AC,AD是它的一条完美分割线,将△ABD沿直线AD折叠后,点B落在点B1处,AB1交CD于点E,求证:DB1=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.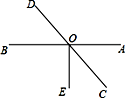
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列说法:①0是整数;②-3.5是负分数;③5.4不是正数;④自然数一定是正数;⑤负分数一定是负有理数,其中正确的有( ).
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A>∠B.
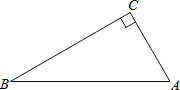
(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值![]() ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.
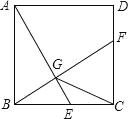
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com