
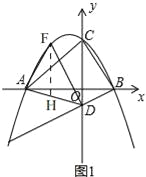
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC

(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
【答案】(1)直线AD解析式为y=﹣![]() x﹣1;(2)N点的横坐标为:﹣
x﹣1;(2)N点的横坐标为:﹣![]() ;(3)PC的值为:
;(3)PC的值为: ![]() 或4﹣
或4﹣![]() 或
或![]() 或
或![]() .
.
【解析】解:(1)∵抛物线y=﹣![]()
![]() x2﹣
x2﹣![]()
![]() x+3与x轴交于A和B两点,
x+3与x轴交于A和B两点,
∴0=﹣![]()
![]() x2﹣
x2﹣![]()
![]() x+3,
x+3,
∴x=2或x=﹣4,
∴A(﹣4,0),B(2,0),
∵D(0,﹣1),
∴直线AD解析式为y=﹣![]()
![]() x﹣1;
x﹣1;
(2)如图1,
过点F作FH⊥x轴,交AD于H,
设F(m,﹣![]()
![]() m2﹣
m2﹣![]()
![]() m+3),H(m,﹣
m+3),H(m,﹣![]()
![]() m﹣1),
m﹣1),
∴FH=﹣![]()
![]() m2﹣
m2﹣![]()
![]() m+3﹣(﹣
m+3﹣(﹣![]()
![]() m﹣1)=﹣
m﹣1)=﹣![]()
![]() m2﹣
m2﹣![]()
![]() m+4,
m+4,
∴S△ADF=S△AFH+S△DFH=![]()
![]() FH×|yD﹣yA|=2FH=2(﹣
FH×|yD﹣yA|=2FH=2(﹣![]()
![]() m2﹣
m2﹣![]()
![]() m+4)=﹣
m+4)=﹣![]()
![]() m2﹣m+8=﹣
m2﹣m+8=﹣![]()
![]() (m+
(m+![]()
![]() )2+
)2+![]()
![]() ,
,
当m=﹣![]()
![]() 时,S△ADF最大,
时,S△ADF最大,
∴F(﹣![]()
![]() ,
,![]()
![]() )
)
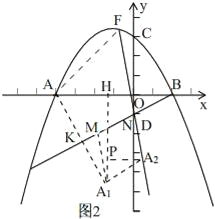
如图2,
作点A关于直线BD的对称点A1,把A1沿平行直线BD方向平移到A2,且A1A2=![]()
![]() ,
,
连接A2F,交直线BD于点N,把点N沿直线BD向左平移![]()
![]() 得点M,此时四边形AMNF的周长最小.
得点M,此时四边形AMNF的周长最小.
∵OB=2,OD=1,
∴tan∠OBD=![]()
![]() ,
,
∵AB=6,
∴AK=![]()
![]() ,
,
∴AA1=2AK=![]()
![]() ,
,
在Rt△ABK中,AH=![]()
![]() ,A1H=
,A1H=![]()
![]() ,
,
∴OH=OA﹣AH=![]()
![]() ,
,
∴A1(﹣![]()
![]() ,﹣
,﹣![]()
![]() ),
),
过A2作A2P⊥A2H,
∴∠A1A2P=∠ABK,
∵A1A2=![]()
![]() ,
,
∴A2P=2,A1P=1,
∴A2(﹣![]()
![]() ,﹣
,﹣![]()
![]() )
)
∵F(﹣![]()
![]() ,
,![]()
![]() )
)
∴A2F的解析式为y=﹣![]()
![]() x﹣
x﹣![]()
![]() ①,
①,
∵B(2,0),D(0,﹣1),
∴直线BD解析式为y=﹣![]()
![]() x﹣1②,
x﹣1②,
联立①②得,x=﹣![]()
![]() ,
,
∴N点的横坐标为:﹣![]()
![]() .
.
(3)∵C(0,3),B(2,0),D(0,﹣1)
∴CD=4,BC=![]()
![]() ,OB=2,
,OB=2,
BC边上的高为DH,
根据等面积法得,![]()
![]() BC×DH=
BC×DH=![]()
![]() CD×OB,
CD×OB,
∴DH=![]()
![]() =
=![]()
![]() ,
,
∵A(﹣4,0),C(0,3),
∴OA=4,OC=3,
∴tan∠ACD=![]()
![]() ,
,
①当PC=PQ时,简图如图1,
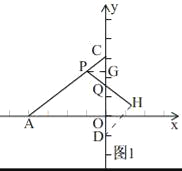

过点P作PG⊥CD,过点D作DH⊥PQ,
∵tan∠ACD=![]()
![]()
∴设CG=3a,则QG=3a,PG=4a,PQ=PC=5a,
∴DQ=CD﹣CQ=4﹣6a
∵△PGQ∽△DHQ,
∴![]()
![]() ,
,
∴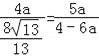
 ,
,
∴a=![]()
![]() ,
,
∴PC=5a=![]()
![]() ;
;
②当PC=CQ时,简图如图2,
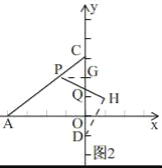

过点P作PGspan>⊥CD,
∵tan∠ACD=![]()
![]()
∴设CG=3a,则PG=4a,
∴CQ=PC=5a,
∴QG=CQ﹣CG=2a,
∴PQ=2![]()
![]() a,
a,
∴DQ=CD﹣CQ=4﹣5a
∵△PGQ∽△DHQ,
同①的方法得出,PC=4﹣![]()
![]() ,
,
③当QC=PQ时,简图如图1
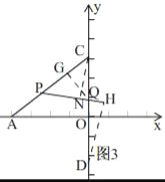

过点Q作QG⊥PC,过点C作CN⊥PQ,
设CG=3a,则QG=4a,PQ=CQ=5a,
∴PG=3a,
∴PC=6a
∴DQ=CD﹣CQ=4﹣5a,
利用等面积法得,CN×PQ=PC×QG,
∴CN=![]()
![]() a,
a,
∵△CQN∽△DQH
同①的方法得出PC=![]()
![]()
④当PC=CQ时,简图如图4,
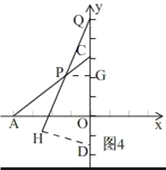

过点P作PG⊥CD,过H作HD⊥PQ,
设CG=3a,则PG=4a,CQ=PC=5a,
∴QD=4+5a,PQ=4![]()
![]() ,
,
∵△QPG∽△QDH,
同①方法得出.CP=![]()
![]()
综上所述,PC的值为:![]()
![]() ;4﹣
;4﹣![]()
![]() ,
,![]()
![]() ,=
,=![]()
![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A.![]()
B.8
C.![]()
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县政府打算用25000元用于为某乡福利院购买每台价格为2000元的彩电和每台价格为1800元的冰箱,并计划恰好全部用完此款.
(1)问原计划所购买的彩电和冰箱各多少台?
(2)由于国家出台“家电下乡”惠农政策,该县政府购买的彩电和冰箱可获得13%的财政补贴,若在不增加县政府实际负担的情况下,能否多购买两台冰箱?谈谈你的想法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是( )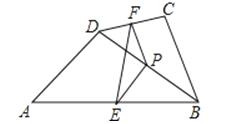
A.120°
B.150°
C.135°
D.140°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com