
 阅读材料:
阅读材料:
科目:初中数学 来源: 题型:填空题
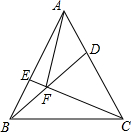 如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.
如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市八年级3月调研考试数学试卷(解析版) 题型:单选题
若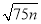 是整数,则正整数n的最小值是( )
是整数,则正整数n的最小值是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com