
【题目】如图1,![]() ,
,![]() 被直线
被直线![]() 所截,点
所截,点![]() 是线段
是线段![]() 上的点,过点
上的点,过点![]() 作
作![]() ,连接
,连接![]() ,
,![]()


(1)试说明![]() .
.
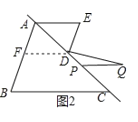
(2)将线段![]() 沿着直线
沿着直线![]() 平移得到线段
平移得到线段![]() ,如图2,连接
,如图2,连接![]() .若
.若![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)见解析(2)15°
【解析】
(1)根据平行线的性质得到∠BAE+∠E=180![]() ,等量代换得到∠BAE+∠B=180
,等量代换得到∠BAE+∠B=180![]() ,于是得到结论;
,于是得到结论;
(2)如图2,过D作DF∥AE交AB于F,根据平行线的性质与周角的性质求出∠FDQ,再根据平行的性质即可得到结论.
(1)∵DE∥AB,
∴∠BAE+∠E=180![]() ,
,
∵∠B=∠E,
∴∠BAE+∠B=180![]() ,
,
∴AE∥BC;
(2)如图2,过D作DF∥AE交AB于F,
∵PQ∥AE,
∴DF∥PQ,
∵![]() ,
,
∴∠EDF=105![]() ,
,
∵DE⊥DQ,
∴∠EDQ=90![]() ,
,
∴∠FDQ=360°105°90°=165°,
∵线段![]() 沿着直线
沿着直线![]() 平移得到线段
平移得到线段![]()
∴DF∥AE∥PQ
∴∠Q=180°-∠FDQ =180°165°=15°.


科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
(3)若该函数的值y随自变量x的增大而减小,求m的取值范围;
(4)该函数图象不经过第二象限,求m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图甲所示.(单位
型两种板材.如图甲所示.(单位![]() )
)
(1)列出方程(组),求出图甲中![]() 与
与![]() 的值;
的值;
(2)在试生产阶段,若将625张标准板材用裁法一裁剪,125张标准板材用裁法二裁剪,再将得到的![]() 型与
型与![]() 型板材做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?
型板材做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化自信”.某校组织全校1000名学生举办了第二届“中华诗词大赛”的初赛,从中抽取部分学生的成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩 | 人数 | 百分比 |
|
| 8 | 20% |
|
| 16 |
|
|
|
| 30% |
|
| 4 | 10% |
频数分布直方图

请观察图表,解答下列问题:
(1)表中![]() __________,
__________,![]() __________;
__________;
(2)补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,那么请你估计该校进入决赛的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
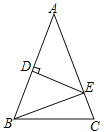
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
(![]() )直线
)直线![]() 、
、![]() 、
、![]() ,如果
,如果![]() 、
、![]() ,那么
,那么![]() .
.
(![]() )三角形的三个内角中至少有两个锐角.
)三角形的三个内角中至少有两个锐角.
(![]() )平移变换中,各组对应点连成的两线段平行(或共线)且相等.
)平移变换中,各组对应点连成的两线段平行(或共线)且相等.
(![]() )三角形的外角和是
)三角形的外角和是![]() .
.
A.(![]() )(
)(![]() )B.(
)B.(![]() )(
)(![]() )C.(
)C.(![]() )(
)(![]() )D.(
)D.(![]() )(
)(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com