练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

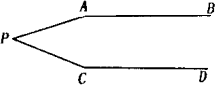
    如图，AB∥CD，探讨∠APC与∠PAB、∠PCD的关系．

    答案：
    解析：

    　　画PQ∥AB

    　　∵AB∥CD

    　　∴PQ∥CD

    　　∵AB∥PQ，∴∠1＋∠A＝180°

    　　∵PQ∥CD，∴∠2＋∠C＝180°

    　　∴∠APC＝∠1＋∠2＝180°－∠A＋180°－∠C＝360°－∠A－∠C

    　　而∠APC＋∠A＋∠C＝360°，即∠APC＋∠PAB＋∠PCD＝360°


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•南湖区二模）在特殊四边形的复习课上，王老师出了这样一道题：
    如图1，在?ABCD中，E、F、G、H分别为AB，BC，CD，DA边上的动点，连接EG，HF相交于点O，且∠HOE=∠ADC，若AB=a，AD=b，试探究：EG与FH的数量关系．
    经过小组讨论后，小聪建议分以下三步进行，请你解答：
    （1）特殊情况，探索结论
    当?ABCD是边长为a的正方形时（如图2），请写出EG与FH的数量关系（不必证明）；
    （2）尝试变题，再探思路
    当?ABCD是边长为a的菱形时（如图3），EG与FH又有怎样的数量关系呢？
    小聪想：要求EG与FH的数量关系，就要构成全等三角形或相似三角形，于是，分别过点G、H作GM⊥AB于点M，HN⊥BC于点N，在△HNF和△GME中，有∠GME=∠HNF=Rt∠，由菱形面积与性质可得GM=HN，能否从已知条件得到∠MGE=∠NHF呢？请你根据小聪的思路完成解答过程；
    （3）特例启发，解答题目
    猜想：原题中EG与FH的数量关系是
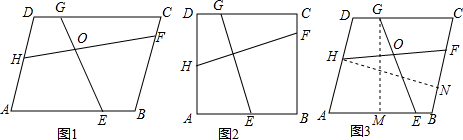
    EG
    FH
    =
    b
    a
    EG
    FH
    =
    b
    a
    ，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：学习周报　数学　沪科九年级版　2009－2010学年　第10期　总第166期 沪科版 题型：044

    “地震无情，人有情”，为了挽救受灾群众的生命，某地震救援队探测出某建筑物废墟下方的点C处有生命迹象．已知废墟一侧地面上的两个探测点A、B相距3米，探测线与地面的夹角分别为30°和60°(如图)，你能确定生命所在点C的深度吗？

    (提示：如图，过点C作CD⊥AB交AB的延长线于点D)．

    方法一：由题意知，∠ACB＝30°．所以△ABC为________三角形．所以BC＝AB＝3米．在Rt△BDC中，∠CBD＝60°，所以CD＝BC·________≈2.6(米)．

    所以生命所在点C的深度约为2.6米．

    方法二：因为探测线与地面的夹角分别为30°、60°，所以∠CAD＝30°，∠CBD＝60°．

    在Rt△BDC中，tan60°＝，所以BD＝________＝________．

    在Rt△ADC中，tan30°＝，所以AD＝________＝________．

    因为AB＝AD－BD＝3米，所以________－________＝3(米)．

    所以CD＝≈2.6(米)．

    所以生命所在点C的深度约为2.6米．

    查看答案和解析>>

    同步练习册答案