
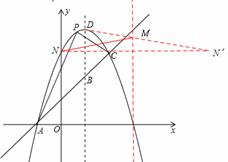
如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E
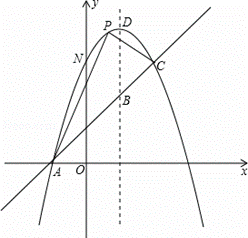
解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,
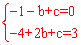 ,解得
,解得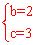 。∴抛物线的函数关系式为
。∴抛物线的函数关系式为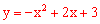 。
。
设直线AC的函数关系式为y=kx+n,由直线AC过点A(﹣1,0)及C(2,3)得
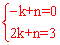 ,解得
,解得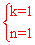 。∴直线AC的函数关系式为y=x+1。
。∴直线AC的函数关系式为y=x+1。
(2)作N点关于直线x=3的对称点N′,令x=0,得y=3,即N(0,3)。∴N′(6, 3)
由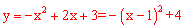 得D(1,4)。
得D(1,4)。
设直线DN′的函数关系式为y=sx+t,则
 ,解得
,解得 。X K b1. C om
。X K b1. C om
∴故直线DN′的函数关系式为 。
。
根据轴对称的性质和三角形三边关系,知当M(3,m)在直线DN′上时,MN+MD的值最小,∴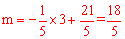 。∴使MN+MD的值最小时m的值为
。∴使MN+MD的值最小时m的值为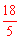 。
。
(3)由(1)、(2)得D(1,4),B(1,2),
①当BD为平行四边形对角线时,由B、C、D、N的坐标知,四边形BCDN是平行四边形,此时,点E与点C重合,即E(2,3)。
②当BD为平行四边形边时,∵点E在直线AC上,∴设E(x,x+1),则F(x,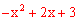 )。又∵BD=2∴若四边形BDEF或BDFE是平行四边形时,BD=EF。
)。又∵BD=2∴若四边形BDEF或BDFE是平行四边形时,BD=EF。
∴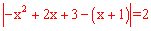 ,即
,即 。
。
若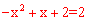 ,解得,x=0或x=1(舍去),∴E(0,1)。
,解得,x=0或x=1(舍去),∴E(0,1)。
若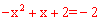 ,解得,
,解得,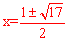 ,∴E
,∴E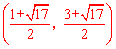 或E
或E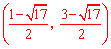 。
。
综上,满足条件的点E为(2,3)、(0,1)、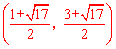 、
、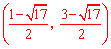 。
。


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
随机抽取某城市30天的空气质量状况统计如下:
污染指数(ω) | 40 | 70 | 90 | 110 | 120 | 140 |
天数(t) | 3 | 5 | 10 | 7 | 4 | 1 |
其中:w≤50时,空气质量为优;50<w≤100时,空气质量为良;100<w≤150时,空气质量为轻微污染.
(1)如果要利用面积分别表示空气质量的优、良及轻微污染,那么这三类空气质量的面积之比为多少?
(2)估计该城市一年(以365天计)中有多少天空气质量达到良以上;
(3)保护环境人人有责,你能说出几种保护环境的好方法吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
一只不透明的口袋里装有红、黄、蓝三种不同颜色的小球若干个(除颜色外其余都相同),其中红球2个,蓝球1个,若从中任意摸出一个球为蓝球的概率为1/4
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回)第二次再摸出一个球。请用画树状图或列表法,求两次摸到不同颜色球的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
利用墙的一边,再用13m的铁丝网,围成一个面积为20 的长方形场地,求这个长方形场地的两边长,设墙的对边长为
的长方形场地,求这个长方形场地的两边长,设墙的对边长为 ,可列方程为 ( )
,可列方程为 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
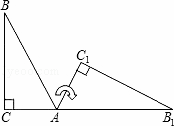
.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
|
| A. | 55° | B. | 125° | C. | 70° | D. | 145° |
查看答案和解析>>
科目:初中数学 来源: 题型:
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,
AC=3,BC=6.
(1)试作出△ABC以A为旋转中心、沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-5,5),试建立合适的直角坐标系,并写出A、C两点的坐标;
(3)作出与△ABC关于原点对称的图形△A2B2C2,并写出A2、B2、C2三点的坐标.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com