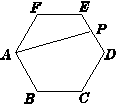
如图11,正六边形ABCDEF中,AB=2,P是ED的中点,连接AP,则AP的长为________.
阅读快车系列答案科目：初中数学 来源： 题型：
如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G，
（1）完成下面的证明：
∵ MG平分∠BMN（ ），
∴ ∠GMN＝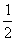
∠BMN（ ），
同理∠G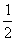NM＝∠DNM．
∵ AB∥CD（ ），
∴ ∠BMN＋∠DNM＝________（ ）．
∴ ∠GMN＋∠GNM＝________．
∵ ∠GMN＋∠GNM＋∠G＝________（ ），
∴ ∠G＝ ________．
∴ MG与NG的位置关系是________．
（2）把上面的题设和结论，用文字语言概括为一个命题：
_______________________________________________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图2，在正方形ABCD中，E为DC边上的点，连接BE，将△BCE绕点C顺时针方向旋转90°得到△DCF，连接EF，若∠BEC＝60°，则∠EFD的度数为（ ）
图2
A.10° B.15° C.20° D.25°
查看答案和解析>>
科目：初中数学 来源： 题型：
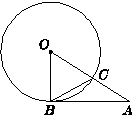
如图1，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO=40°，则∠OCB的度数为（ ）
A．40° B．50° C．65° D．75°
查看答案和解析>>
科目：初中数学 来源： 题型：
如图6，将边长为1 cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为（ ）
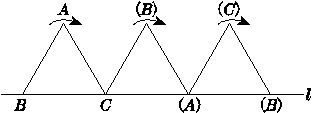
图6
A．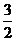
π cm B．
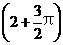cm C．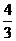
π cm D．3 cm
查看答案和解析>>
科目：初中数学 来源： 题型：
如图16，在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与x轴相交于点A，与y轴相交于点B．
（1）点P在运动时，线段AB的长度也在发生变化，请写出线段AB长度的最小值，并说明理由；
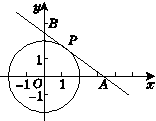
（2）在⊙O上是否存在一点Q，使得以Q，O，A，P为顶点的四边形是平行四边形？若存在，请求出Q点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
在学习概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是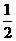
”，小明做了下列三个模拟试验来验证．
①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值；
②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值；
③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥（如图4），从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值．
上面的试验中，不科学的有（ ）
A．0个 B．1个 C．2个 D．3个
查看答案和解析>>
科目：初中数学 来源： 题型：
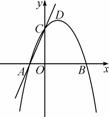
综合与探究：如图，在平面直角坐标系中，抛物线y＝－x2＋2x＋3与x轴交于A、B两点，与y轴交于点C，点
D是该抛物线的顶点．
(1)求直线AC的解析式及B、D两点的坐标；
(2)点P是x轴上一个动点，过P作直线l∥AC交抛物线于点Q.试探究：随着P点的运动，在抛物线上是否存在点Q，使以点A、P、Q、C为顶点的四边形是平行四边形，若存在，请直接写出符合条件的点Q的坐标；若不存在，请说明理由；
(3
)请在直线AC上找一点M，使△BDM的周长最小，求出M点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
点拨： 连接AE，如答图4,由题意易得AE=2
,EP=1, ∠AEP=90°.∴在Rt△AEP中，
= 
=
π