
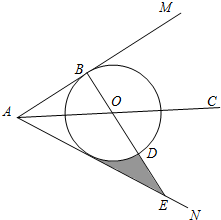
 如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.
如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.分析 (1)首先过点O作OF⊥AN于点F,易证得OF=OB,即可得AN是⊙O的切线;
(2)由∠MAN=60°,OB⊥AM,可求得OF的长,又由S阴影=S△OEF-S扇形OFD,即可求得答案.
解答 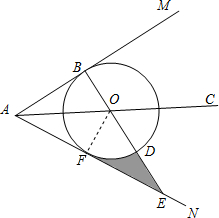 (1)证明:过点O作OF⊥AN于点F,
(1)证明:过点O作OF⊥AN于点F,
∵⊙O与AM相切于点B,
∴OB⊥AM,
∵AC平分∠MAN,
∴OF=OB=1,
∴AN是⊙O的切线;
(2)解:∵∠MAN=60°,OB⊥AM,
∴∠AEB=30°,
∴OF⊥AN,
∴∠FOE=60°,
在Rt△OEF中,tan∠FOE=$\frac{FE}{OF}$,
∴EF=OF•tan60°=$\sqrt{3}$,
∴S阴影=S△OEF-S扇形ODF=$\frac{1}{2}$OF•EF-$\frac{60}{360}$×π×OF2=$\frac{\sqrt{3}}{2}$-$\frac{1}{6}$π.
点评 此题考查了切线的判定与性质、扇形的面积以及三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | 18,18,3 | B. | 18,18,1 | C. | 18,17.5,3 | D. | 17.5,18,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CN}$的值为( )
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CN}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
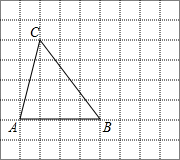 作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1
作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com