
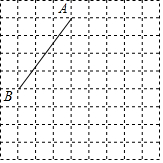
 如图,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
如图,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)直接建立坐标系得出答案;
(3)直接利用扇形面积公式求法进而得出答案;
(4)直接利用弧长等于圆锥的底面周长进而得出答案.
解答 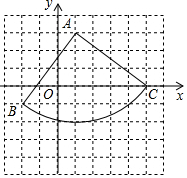 解:(1)如图所示:点B经过的路径为弧BC;
解:(1)如图所示:点B经过的路径为弧BC;
(2)如图所示:点C的坐标为:(5,0);
故答案为:(5,0);
(3)线段AB在旋转到线段AC的过程中,线段AB扫过区域的面积为:$\frac{90π×{5}^{2}}{360}$=$\frac{25π}{4}$;
故答案为:$\frac{25π}{4}$;
(4)设该圆锥底面圆的半径长为r,
由题意可得:$\widehat{CB}$=$\frac{90π×5}{180}$=$\frac{5}{2}$π,
则2πr=$\frac{5}{2}$π,
解得:r=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 此题主要考查了旋转变换以及扇形面积和弧长公式应用,正确得出对应点位置是解题关键.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)4×(-1)3=-1 | B. | -(-3)3=27 | C. | $\frac{1}{3}$÷(-$\frac{1}{3}$)3=9 | D. | -3÷(-$\frac{1}{3}$)=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
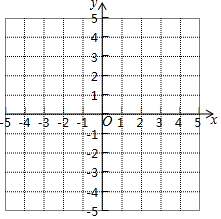 已知二次函数y=x2-2x.
已知二次函数y=x2-2x.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(b-5)=ab-5a | B. | a2-4a+4=a(a-4)+4 | ||
| C. | x2-81y2=(x+9y)(x-9y) | D. | (3x-2)(2x+1)=6x2-x-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com