
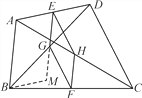
【题目】在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(提示:过点B作BM∥AD交EG的延长线于点M,证明EG//AB且EG=![]() AB)
AB)
【答案】见解析
【解析】试题分析:本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=![]() CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
试题解析:当AB=CD时,四边形EGFH为菱形.
证明:过点B作BM∥AD交EG的延长线于点M,则∠DEG=∠GMB.∵G为BD的中点,∴DG=GB.
又∵∠DGE=∠BGM,∴△DGE≌△BGM,∴EG=GM,ED=BM.
∵E为AD的中点,∴AE=ED,∴BM∥AE,
∴四边形AEMB为平行四边形,
∴EM∥AB,
∴EG∥![]() AB,EG=
AB,EG=![]() AB.
AB.
同理FH∥![]() CD,GF∥
CD,GF∥![]() CD,GF=
CD,GF=![]() CD,
CD,
∴四边形EGFH为平行四边形.
∵AB=CD,∴GF=HF,
∴平行四边形EGHF是菱形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
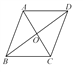
【题目】已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
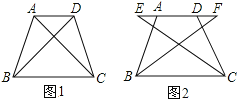
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”.21:00至次日8:00是用电低谷期,简称“谷时”为了缓解供电需求的矛盾,某市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:

小明家对换表后最初使用的95千瓦·时电进行测算,发现比在换表前使用95千瓦·时电节约了5.9元,小明家使用“峰时”电和“谷时”电分别是多少千瓦·时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com