
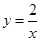 , 0<x<1;(2)能,此时BE的长为
, 0<x<1;(2)能,此时BE的长为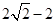 或
或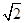
 ,再由
,再由 ,
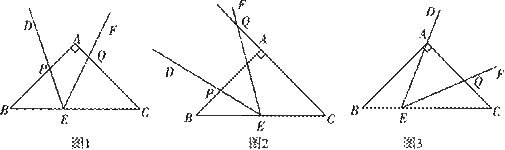
,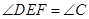 可证得△BPE∽△CEQ,根据相似三角形的性质可得
可证得△BPE∽△CEQ,根据相似三角形的性质可得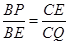 ,设BP为x,CQ为y,即得
,设BP为x,CQ为y,即得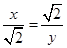 ,从而可以求得结果;
,从而可以求得结果;
 ,
,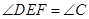
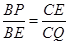
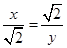
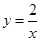 ,自变量x的取值范围是0<x<1;
,自变量x的取值范围是0<x<1;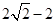
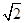
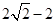 或
或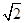 .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
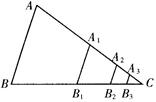
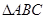 的面积为1,分别取AC、BC两边中点A1、B1,四边形A1ABB1的面积为____________,再分别取A1C、B1C的中点A2、B2;又再取A2C、B2C的中点A3、B3;依次取下去……,利用这一图形能直观地计算出
的面积为1,分别取AC、BC两边中点A1、B1,四边形A1ABB1的面积为____________,再分别取A1C、B1C的中点A2、B2;又再取A2C、B2C的中点A3、B3;依次取下去……,利用这一图形能直观地计算出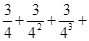 ……
……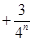 = .
= . 
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
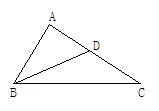
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.4cm、2cm、1cm、3cm | B.1cm、2cm、3cm、4cm |
| C.25cm、35cm、45cm、55cm | D.1cm、2cm、20cm、40cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com