



科目:初中数学 来源:不详 题型:解答题
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。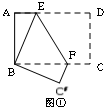
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
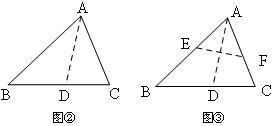
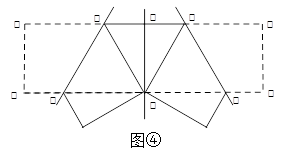
 的顶点都在格点上,且△
的顶点都在格点上,且△ 与△
与△ 关于点
关于点 成中心对称.
成中心对称.
 的位置;
的位置;  沿水平方向向右平移5个单位后的△
沿水平方向向右平移5个单位后的△ .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

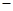 ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com