
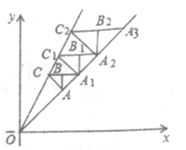
【题目】如图,在平面直角坐标系第一象限内,直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,使
,使![]() ,边
,边![]() 轴,
轴,![]() 轴,
轴,![]() 在直线
在直线![]() 上,点C在直线
上,点C在直线![]() 上,CB的延长线交直线
上,CB的延长线交直线![]() 于点
于点![]() ,作等腰
,作等腰![]() ,使
,使![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,按此规律,则等腰
上,按此规律,则等腰![]() 的腰长为_______.
的腰长为_______.
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
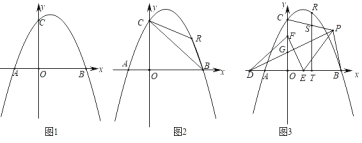
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
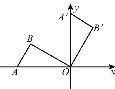
【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
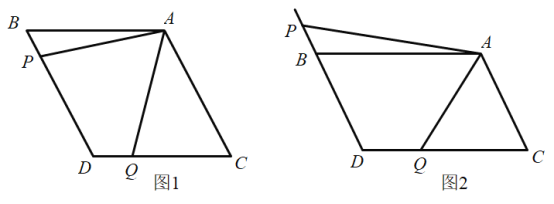
【题目】如图1,![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,且满足
上的点,且满足![]() .
.
(1)求证:![]()
(2)在图1中,是否存在与AP相等的线段?若存在,请找出来,并加以证明;若不存在,说明理由.
(3)若将“![]() 为
为![]() 上的点”改为:“
上的点”改为:“![]() 为DB延长线上的点”其他条件不变(如图2)若
为DB延长线上的点”其他条件不变(如图2)若![]() ,求线段
,求线段![]() 之间的数量关系(用含
之间的数量关系(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求![]() 的值;
的值;
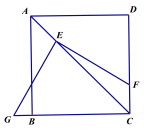
(2)如图,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
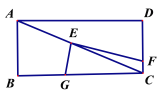
(3)如图,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,直接写出EG、EF 的长.
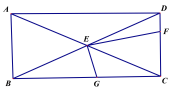
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当白色小正方形个数按![]() 等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第
等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第![]() 个图形中白色小正方形和黑色小正方形的个数总和等于______.(用
个图形中白色小正方形和黑色小正方形的个数总和等于______.(用![]() 表示,
表示,![]() 是正整数)
是正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
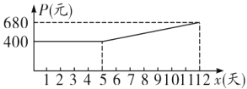
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com