
 如图,在矩形ABCD中,AD=3,以顶点D为圆心,1为半径作⊙D,过边BC上的一点P作射线PQ与⊙D相切于点Q,且交边AD于点M,连接AP,若AP+PQ=2$\sqrt{6}$,∠APB=∠QPC,则∠QPC 的大小约为64度40分.(参考数据:sin11°32′=$\frac{1}{5}$,tan36°52′=$\frac{3}{4}$)
如图,在矩形ABCD中,AD=3,以顶点D为圆心,1为半径作⊙D,过边BC上的一点P作射线PQ与⊙D相切于点Q,且交边AD于点M,连接AP,若AP+PQ=2$\sqrt{6}$,∠APB=∠QPC,则∠QPC 的大小约为64度40分.(参考数据:sin11°32′=$\frac{1}{5}$,tan36°52′=$\frac{3}{4}$) 分析 作辅助线,构建直角三角形DQN,先得出NQ=AP+PQ=2$\sqrt{6}$,再由勾股定理求出DN的长,分别在Rt△AND和Rt△NQD中,根据三角函数求∠AND和∠DNQ的度数,得出结论.
解答 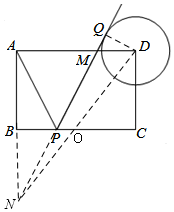 解:如图,延长MP和AB交于点N,连接DN、DQ,
解:如图,延长MP和AB交于点N,连接DN、DQ,
∵射线PQ与⊙D相切于点Q,
∴DQ⊥NQ,DQ=1,
∵∠APB=∠QPC,∠QPC=∠BPN,
∴∠APB=∠BPN,
∵BP⊥AN,
∴AP=PN,
∴NQ=AP+PQ=2$\sqrt{6}$,
由勾股定理得:DN=$\sqrt{(2\sqrt{6})^{2}+{1}^{2}}$=5,AN=$\sqrt{{5}^{2}-{3}^{2}}$=4,
在Rt△AND中,tan∠AND=$\frac{AD}{AN}$=$\frac{3}{4}$,
∵tan36°52′=$\frac{3}{4}$,
∴∠AND=36°52′,
在Rt△NQD中,sin∠DNQ=$\frac{DQ}{DN}$=$\frac{1}{5}$,
∵sin11°32′=$\frac{1}{5}$,
∴∠DNQ=11°32′,
∴∠BNP=36°52′-11°32′=25°20′,
∴∠QPC=∠BPN=90°-25°20′=64°40′.
故答案为:64,40.
点评 本题综合考查了切线、矩形的性质,利用勾股定理求边长,并根据条件解直角三角形;在几何证明中,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.


科目:初中数学 来源: 题型:解答题
 已知,点A(-2,1),B(-3,0),C(-1,1).请在平面直角坐标系xOy中分别标出点A,B,C的位置,顺次连接A、B、C三点,并将三角形ABC向右平移3个单位,向下平移1个单位,画出平移后的图形.
已知,点A(-2,1),B(-3,0),C(-1,1).请在平面直角坐标系xOy中分别标出点A,B,C的位置,顺次连接A、B、C三点,并将三角形ABC向右平移3个单位,向下平移1个单位,画出平移后的图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC绕顶点C旋转某一个角度后得到△A′B′C,问:
如图,△ABC绕顶点C旋转某一个角度后得到△A′B′C,问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com