
 .
.
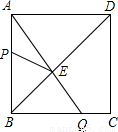
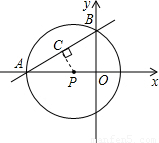 解:(1)作PC⊥AB于点C.
解:(1)作PC⊥AB于点C.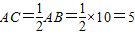 ,
,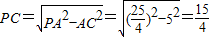 .
.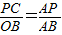 即
即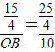 .
.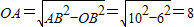 .
.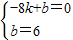 .∴
.∴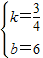 .
.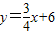 .
.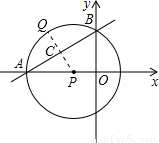
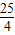 ,
,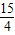 ,CQ=PQ-PC=
,CQ=PQ-PC=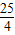 -
-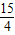 =
= ,
,

科目:初中数学 来源:2010年北京市实验外国语学校中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年上海市青浦区中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年上海市青浦区中考数学二模试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:2009年上海市青浦区中考数学二模试卷(解析版) 题型:解答题
 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com