
”¾ĢāÄæ”æŅŃÖŖ”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬AC=BC=2£¬DŹĒ±ßABÉĻŅ»¶Æµć£ØA”¢BĮ½µć³żĶā£©£¬½«”÷CADČʵćC°“ÄꏱÕė·½ĻņŠż×Ŗ½Ē¦ĮµĆµ½”÷CEF£¬ĘäÖŠµćEŹĒµćAµÄ¶ŌÓ¦µć£¬µćFŹĒµćDµÄ¶ŌÓ¦µć£®
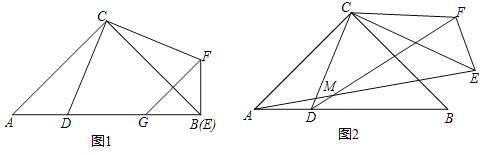
£Ø1£©ČēĶ¼1£¬µ±¦Į=90”揱£¬GŹĒ±ßABÉĻŅ»µć£¬ĒŅBG=AD£¬Į¬½ÓGF£®ĒóÖ¤£ŗGF”ĪAC£»
£Ø2£©ČēĶ¼2£¬µ±90”ć”ܦĮ”Ü180”揱£¬AEÓėDFĻą½»ÓŚµćM£®
¢Łµ±µćMÓėµćC”¢D²»ÖŲŗĻŹ±£¬Į¬½ÓCM£¬Ēó”ĻCMDµÄ¶ČŹż£»
¢ŚÉčDĪŖ±ßABµÄÖŠµć£¬µ±¦Į“Ó90”ć±ä»Æµ½180”揱£¬ĒóµćMŌĖ¶ÆµÄĀ·¾¶³¤£®
”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£»£Ø2£©¢Ł135”ć£»¢Ś![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓūÖ¤Ć÷GF”ĪAC£¬Ö»ŅŖÖ¤Ć÷”ĻA=”ĻFGB¼“æɽā¾öĪŹĢā£®
£Ø2£©¢ŁĻČÖ¤Ć÷A”¢D”¢M”¢CĖÄµć¹²Ō²£¬µĆµ½”ĻCMF=”ĻCAD=45”ć£¬¼“æɽā¾öĪŹĢā£®
¢ŚĄūÓĆ¢ŁµÄ½įĀŪæÉÖŖ£¬µćMŌŚŅŌACĪŖÖ±¾¶µÄ”ŃOÉĻ£¬ŌĖ¶ÆĀ·¾¶ŹĒ»”CD£¬ĄūÓĆ»”³¤¹«Ź½¼“æɽā¾öĪŹĢā£®
ŹŌĢā½āĪö£ŗ£Ø1£©ČēĶ¼1ÖŠ£¬”ßCA=CB£¬”ĻACB=90”ć£¬”ą”ĻA=”ĻABC=45”ć£¬”ß”÷CEFŹĒÓÉ”÷CADŠż×ŖÄꏱÕė¦ĮµĆµ½£¬¦Į=90”ć£¬”ąCBÓėCEÖŲŗĻ£¬”ą”ĻCBE=”ĻA=45”ć£¬”ą”ĻABF=”ĻABC+”ĻCBF=90”ć£¬”ßBG=AD=BF£¬”ą”ĻBGF=”ĻBFG=45”ć£¬”ą”ĻA=”ĻBGF=45”ć£¬”ąGF”ĪAC£®

£Ø2£©¢ŁČēĶ¼2ÖŠ£¬”ßCA=CE£¬CD=CF£¬”ą”ĻCAE=”ĻCEA£¬”ĻCDF=”ĻCFD£¬”ß”ĻACD=”ĻECF£¬”ą”ĻACE=”ĻCDF£¬”ß2”ĻCAE+”ĻACE=180”ć£¬2”ĻCDF+”ĻDCF=180”ć£¬”ą”ĻCAE=”ĻCDF£¬”ąA”¢D”¢M”¢CĖÄµć¹²Ō²£¬”ą”ĻCMF=”ĻCAD=45”ć£¬”ą”ĻCMD=180”ć©”ĻCMF=135”ć£®
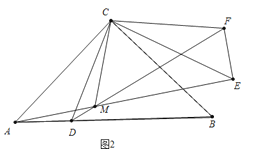
¢ŚČēĶ¼3ÖŠ£¬OŹĒACÖŠµć£¬Į¬½ÓOD”¢CM£®
”ßAD=DB£¬CA=CB£¬”ąCD”ĶAB£¬”ą”ĻADC=90”ć£¬ÓÉ¢ŁæÉÖŖA”¢D”¢M”¢CĖÄµć¹²Ō²£¬”ąµ±¦Į“Ó90”ć±ä»Æµ½180”揱£¬µćMŌŚŅŌACĪŖÖ±¾¶µÄ”ŃOÉĻ£¬ŌĖ¶ÆĀ·¾¶ŹĒ»”CD£¬”ßOA=OC£¬CD=DA£¬”ąDO”ĶAC£¬”ą”ĻDOC=90”ć£¬”ą![]() µÄ³¤=
µÄ³¤=![]() =
=![]() £¬”ąµ±¦Į“Ó90”ć±ä»Æµ½180”揱£¬µćMŌĖ¶ÆµÄĀ·¾¶³¤ĪŖ
£¬”ąµ±¦Į“Ó90”ć±ä»Æµ½180”揱£¬µćMŌĖ¶ÆµÄĀ·¾¶³¤ĪŖ![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄæĒ°ĪŅ¹ś½ØĮ¢ĮĖ±Č½ĻĶźÉĘµÄ¾¼ĆĄ§ÄŃѧɜ׏֜ĢåĻµ£®Ä³Š£Č„ÄźÉĻ°ėÄź·¢·ÅøųĆæøö¾¼ĆĄ§ÄŃѧɜ389ŌŖ£¬½ńÄźÉĻ°ėÄź·¢·ÅĮĖ438ŌŖ£¬ÉčĆæ°ėÄź·¢·ÅµÄ׏֜½š¶īµÄĘ½¾łŌö³¤ĀŹĪŖx£¬ŌņĻĀĆęĮŠ³öµÄ·½³ĢÖŠÕżČ·µÄŹĒ£Ø””””£©
A. 438£Ø1+x£©2=389 B. 389£Ø1+x£©2=438
C. 389£Ø1+2x£©2=438 D. 438£Ø1+2x£©2=389
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø ””””£©
A. °ėŌ²ŹĒ»”£¬»”Ņ²ŹĒ°ėŌ² B. ČżµćČ·¶ØŅ»øöŌ²
C. Ę½·ÖĻŅµÄÖ±¾¶“¹Ö±ÓŚĻŅ D. Ö±¾¶ŹĒĶ¬Ņ»Ō²ÖŠ×ī³¤µÄĻŅ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»¼ŅÉĢµź½ųŠŠ×°ŠŽ£¬ČōĒė¼×”¢ŅŅĮ½øö×°ŠŽ×éĶ¬Ź±Ź©¹¤£¬8ĢģæÉŅŌĶź³É£¬Ščø¶øųĮ½×é·ŃÓĆ¹²3520ŌŖ£»ČōĻČĒė¼××鵄¶Ą×ö6Ģģ£¬ŌŁĒėŅŅ×鵄¶Ą×ö12ĢģæÉŅŌĶź³É£¬Ščø¶øųĮ½×é·ŃÓĆ¹²3480ŌŖ£¬ĪŹ£ŗ
£Ø1£©¼×”¢ŅŅĮ½×鵄¶Ą¹¤×÷Ņ»Ģģ£¬ÉĢµźÓ¦ø÷ø¶¶ąÉŁŌŖ£æ
£Ø2£©ŅŃÖŖ¼××鵄¶ĄĶź³ÉŠčŅŖ12Ģģ£¬ŅŅ×鵄¶ĄĶź³ÉŠčŅŖ24Ģģ£¬µ„¶ĄĒėÄÄ×飬ÉĢµźÓ¦ø¶·ŃÓĆ½ĻÉŁ£æ
£Ø3£©Čō×°ŠŽĶźŗó£¬ÉĢµźĆæĢģæÉÓÆĄū200ŌŖ£¬ÄćČĻĪŖČēŗĪ°²ÅÅŹ©¹¤ÓŠĄūÓĆÉĢµź¾ÓŖ£æĖµĖµÄćµÄĄķÓÉ.£ØæÉŅŌÖ±½ÓÓĆ£Ø1£©£Ø2£©ÖŠµÄŅŃÖŖĢõ¼ž£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć(a-1)2µÄ½į¹ūŹĒ£Ø £©
A. a2-1 B. a2+1 C. a2-2a+1 D. a2+2a-1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠ¼ĘĖćÕżČ·µÄŹĒ £Ø £©
A. a2£«a2£½a4 B. (a2)3£½a5 C. a£«2£½2a D. (ab)3£½a3b3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĢ劣ŅŖ“ÓĖÄĆūÉä»÷Ń”ŹÖÖŠŃ”°ĪŅ»Ćū²Ī¼ÓŹ”ĢåÓżŌĖ¶Æ»į£¬Ń”°ĪČüÖŠĆæĆūŃ”ŹÖĮ¬ŠųÉä°Š10“Ī£¬ĖūĆĒø÷×ŌµÄĘ½¾ł³É¼Ø![]() ¼°Ęä·½²īS2Čē±ķĖłŹ¾£ŗ
¼°Ęä·½²īS2Čē±ķĖłŹ¾£ŗ
¼× | ŅŅ | ±ū | ¶” | |
£Ø»·£© | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
Čē¹ūŅŖŃ”³öŅ»Ćū³É¼ØøßĒŅ·¢»ÓĪČ¶ØµÄŃ”ŹÖ²ĪČü£¬ŌņӦєŌńµÄŃ”ŹÖŹĒ£Ø £©
A£®¼× B£®ŅŅ C£®±ū D£®¶”
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy=©![]() xÓė·“±ČĄżŗÆŹży=
xÓė·“±ČĄżŗÆŹży=![]() µÄĶ¼Ļó½»ÓŚ¹ŲÓŚŌµć¶Ō³ĘµÄA£¬BĮ½µć£¬ŅŃÖŖAµćµÄׯ×ų±źŹĒ3£®
µÄĶ¼Ļó½»ÓŚ¹ŲÓŚŌµć¶Ō³ĘµÄA£¬BĮ½µć£¬ŅŃÖŖAµćµÄׯ×ų±źŹĒ3£®
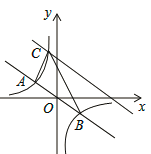
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©½«Ö±Ļßy=©![]() xĻņÉĻĘ½ŅĘŗóÓė·“±ČĄżŗÆŹżŌŚµŚ¶žĻóĻŽÄŚ½»ÓŚµćC£¬Čē¹ū”÷ABCµÄĆ껿ĪŖ48£¬ĒóĘ½ŅĘŗóµÄÖ±ĻßµÄŗÆŹż±ķ“ļŹ½£®
xĻņÉĻĘ½ŅĘŗóÓė·“±ČĄżŗÆŹżŌŚµŚ¶žĻóĻŽÄŚ½»ÓŚµćC£¬Čē¹ū”÷ABCµÄĆ껿ĪŖ48£¬ĒóĘ½ŅĘŗóµÄÖ±ĻßµÄŗÆŹż±ķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com