Question

如图，AB＝AC，AD＝AE．

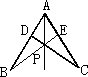
求证：∠B＝∠C．

Answer 1

答案：
解析：

利用全等三角形的知识，同学们很快就可以证明∠B＝∠C．但我们继续思考：假设线段BE与线段CD相交于点P，那么射线AP是否平分∠BAC？经过推理，可知AP是∠BAC的平分线．由此我们得到角的平分线的又一种作法． 　　已知：∠AOB． 　　求作：∠AOB的平分线． 　　作法：(1)以点O为圆心，任意长为半径作弧，交OA于点C，交OB于点D． 　　(2)再以点O为圆心，适当长为半径作弧(长度与(1)中不同)，交OA于点E，交OB于点F． 　　(3)连接CF、DE，CF与DE交于点P． 　　(4)作射线OP．则射线OP即为所求(如图)． 　　反思：作法已经介绍完了，那么这种作法的道理何在呢？下面给出此题的证明思路． 　　思路：过点P分别作AO与BO的垂线，垂足为M、N．如图所示．首先由作法可得CE＝DF，△FOC≌△EOD．所以S△FOC＝S△EOD．进而可得S△EPC＝S△FPD．因为CE＝DF，所以PM＝PN．所以由“到角的两边距离相等的点在这个角的平分线上”可得点P在∠AOB的平分线上，即OP为∠AOB的平分线． 　　点评：(1)利用三角形全等和“到角的两边距离相等的点在这个角的平分线上”证明某线为角的平分线是一种常见的证明方法； 　　(2)利用面积法来证明垂线段相等是一种常见的证明线段相等的方法．