23、先阅读下面材料,然后解答问题:
材料一:如图(1),直线l上有A
1、A
2两个点,若在直线l上要确定一点P,且使点P到点A
1、A
2的距离之和最小,很明显点P的位置可取在A
1和A
2之间的任何地方,此时距离之和为A
1到A
2的距离.
如图(2),直线l上依次有A
1、A
2、A
3三个点,若在直线l上要确定一点P,且使点P到点A
1、A
2、A
3的距离之和最小,不难判断,点P的位置应取在点A
2处,此时距离之和为A
1到A
3的距离.(想一想,这是为什么)
不难知道,如果直线l上依次有A
1、A
2、A
3、A
4四个点,同样要确定一点P,使它到各点的距离之和最小,则点P应取在点A
2和A
3之间的任何地方;如果直线l上依次有A
1、A
2、A
3、A
4、A
5五个点,则相应点P的位置应取在点A
3的位置.

材料二:数轴上任意两点a、b之间的距离可以表示为|a-b|.
问题一:若已知直线l上依次有点A
1、A
2、A
3、…、A
25共25个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在
点A13处
;
若已知直线l上依次有点A
1、A
2、A
3、…、A
50共50个点,要确定一点P,使它到已知各点的距离之和最小,则点P的位置应取在
点A25和A26之间的任何地方
.
问题二:现要求|x+1|+|x|+|x-1|+|x-2|+|x-3|+…+|x-97|的最小值,
根据问题一的解答思路,可知当x值为
49
时,上式有最小值为
1225
.




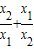 的值.
的值. ,x1x2=2.
,x1x2=2.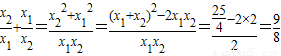
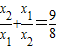 .
. 的值.
的值. ,x1x2=2.
,x1x2=2.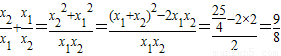
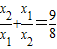 .
.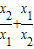 的值.
的值. ,x1x2=2.
,x1x2=2.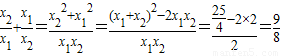
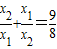 .
.