
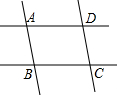
 如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.
如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
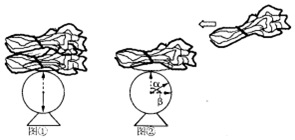 王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:
王老师到菜市场买菜,发现若把10千克的菜放到某秤上,秤的指针盘上的指针转了,如图①所示;于是王老师在学完一元一次方程和角的相关知识后给学生提出了两个问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 21-14$\sqrt{2}$ | B. | 21+14$\sqrt{2}$ | C. | 21+14$\sqrt{2}$或21-14$\sqrt{2}$ | D. | 3+2$\sqrt{2}$或21+14$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
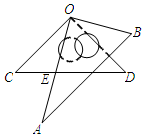 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,CD与OA交于点E,已知∠A=30°,则∠DEO的度数为( )| A. | 45° | B. | 60° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有一长为60cm,宽为40cm的长方形硬纸片,小明在长方形纸片的四个角个剪去一个相同的小正方形,做成一个无盖的长方形盒子.
如图,有一长为60cm,宽为40cm的长方形硬纸片,小明在长方形纸片的四个角个剪去一个相同的小正方形,做成一个无盖的长方形盒子.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
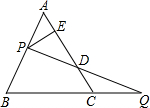 如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.
如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com