
����Ŀ��С����ij���й���A��B��C������Ʒ������A��B������Ʒ�ĵ���֮�����õ���C��Ʒ�ĵ��ۣ�С��ǰ���ι�����Ʒ���������ܷ������±���
��ƷA������ | ��ƷB������ | ��ƷC������ | �ܷ��ã�Ԫ�� | |
��һ�� | 2 | 3 | 2 | 230 |
�ڶ��� | 1 | 4 | 3 | 290 |
��1����A��B��C������Ʒ�ĵ��ۣ�
��2����С����������Ҫ����A��B��C������Ʒ��m��������C��Ʒ��������A��Ʒ��������2����ǡ�û���480ԪǮ��
����m�����ֵ��
����С���ڵ����ι���A��B��C������Ʒʱ������������һ��һ�����������һ��C��Ʒ��������һ��A��Ʒ��һ��B��Ʒ����������A��Ʒ������m��ֵ��
���𰸡���1��A��B��C������Ʒ�ĵ��۷ֱ�Ϊ20Ԫ��30Ԫ��50Ԫ����2����m�����ֵΪ15����m =18
��������
��1����A��B��C������Ʒ�ĵ��۷ֱ�ΪxԪ��yԪ��(x+y)Ԫ���������ι�����Ʒ�ķ��ý�����������⣻
��2����������ι���A��Ʒa����B��Ʒb����C��Ʒ2a������m=3a+b�������ܷ���480Ԫ�������̣�����m����ֵ��
��������������ۣ���a��bʱ������C��Ʒ2a�����ɣ���a<bʱ��A���ù��������ͣ�BֻҪ����(b��a)�����з�����⣮
��1����A��B��C������Ʒ�ĵ��۷ֱ�ΪxԪ��yԪ��(x+y)Ԫ��
��������ã�![]() ��
��
�ã�![]() ������x+y=20+30=50��
������x+y=20+30=50��
��A��B��C������Ʒ�ĵ��۷ֱ�Ϊ20Ԫ��30Ԫ��50Ԫ��
��2��������ι���A��Ʒa����B��Ʒb����C��Ʒ2a����
��m=3a+b��
��20a+30b+50��2a=480���ã�4a+b=16��
��a��b�����������������![]() ��
��![]() ��
��![]() ��
��
��m�����ֵΪ15��
����a��bʱ������C��Ʒ2a�����ɣ�50��2a=480���������⣩
��a<bʱ��A���ù��������ͣ�BֻҪ����(b��a)��
��30(b��a)+50��2a=480��
��a��b�����������������![]() ����m=3a+b=18��
����m=3a+b=18��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������CEFG�߳��ֱ�Ϊa��b��������CEFG�Ƶ�C��ת���������н��ۣ���BE=DG����BE��DG����DE2+BG2=2a2+b2 �� ������ȷ������������ţ�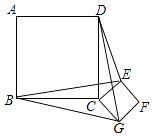
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����A��B��C���У�AB=A��B�䣬��B=��B���������������Բ�һ���ܱ�֤��ABC�ա�A��B��C���������������ǣ� ��

A. BC=B��C�� B. ��A=��A�� C. AC=A��C�� D. ��C=��C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
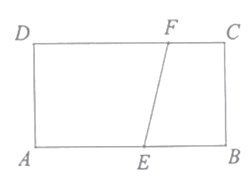
����Ŀ����ͼ����![]() �ֱ�Ϊ������
�ֱ�Ϊ������![]() �ı�
�ı�![]() �ͱ�
�ͱ�![]() �ϵ�һ�����㣬���ı���
�ϵ�һ�����㣬���ı���![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() ǡ������
ǡ������![]() ������
������![]() �����ʱ
�����ʱ![]() �Ķ���Ϊ____��
�Ķ���Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ũ����˾��30Ԫ/ǧ�˵ļ۸��չ�һ��ũ��Ʒ�������ۣ�Ϊ�˵õ���������p��ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵ�������г������ò����������±���
���ۼ۸�x��Ԫ/ǧ�ˣ� | 30 | 35 | 40 | 45 | 50 |
��������p��ǧ�ˣ� | 600 | 450 | 300 | 150 | 0 |
��1��������ݱ��е����ݣ�����ѧ����һ�κ��������κ�����������������֪ʶȷ��p��x֮��ĺ�������ʽ��
��2��ũ����˾Ӧ�����ȷ������ũ��Ʒ�����ۼ۸���ʹ�������������
��3����ũ����˾ÿ����1ǧ������ũ��Ʒ��֧��aԪ��a��0������ط��ã���40��x��45ʱ��ũ����˾���ջ��������ֵΪ2430Ԫ����a��ֵ�����ջ���=������������֧�����ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���BAC��120�㣬ADƽ�֡�BAC����AD��AB������EDF��60���������߷ֱ�AB��AC�ڵ�E��F��
��1����֤����ABD�ǵȱ������Σ�
��2����֤��BE��AF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ������
������![]() ���㷽����
���㷽����![]() ��
��
��1������![]() ��
��![]() ��ľ���Ϊ6����
��ľ���Ϊ6����![]() ��ֵΪ_________��
��ֵΪ_________��
��2������![]() ���߶�
���߶�![]() ��
��![]() �᷽������ƽ�Ƶ��߶�
�᷽������ƽ�Ƶ��߶�![]() �����
�����![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ_______���߶�
�ľ���Ϊ_______���߶�![]() ɨ�������Ϊ15�����
ɨ�������Ϊ15�����![]() ƽ�ƺ��Ӧ��
ƽ�ƺ��Ӧ��![]() ��������Ϊ_______��
��������Ϊ_______��
��3������![]() ��
��![]() ��
��![]() ����
����![]() �����С�ڵ���12����
�����С�ڵ���12����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
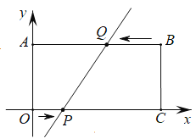
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�ı�OC��OA�ֱ���x�ᡢy���ϣ�B���ڵ�һ���ޣ���A�������ǣ�0��4����OC=8��
��1��ֱ��д����B��C�����ꣻ
��2����P��ԭ��O�������ڱ�OC����ÿ��1����λ���ȵ��ٶ�������C���ƶ���ͬʱ��Q�ӵ�B�������ڱ�BA����ÿ��2����λ���ȵ��ٶ�������A���ƶ�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�ƶ������ƶ���ʱ��Ϊt���ӣ�̽���������⣺
�� ��tֵΪ����ʱ��ֱ��PQ��y�
�� �������˶������У��ܷ�ʹ���ı���BCPQ������dz�����OABC�������![]() �����ܣ���ֱ��д��P��Q��������ꣻ�����ܣ�˵��������
�����ܣ���ֱ��д��P��Q��������ꣻ�����ܣ�˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������[a]��ʾ������a��������������磺[3.5]��3��[4]��4��[��1.5]����2����{a}��ʾ����a����С���������磺{3.5}��4��{1}��2��{��2.5}����2.����������⣺
(1)[��5.5]���ڶ��٣�{2.5}���ڶ��٣�
(2)��[x]��3��д��x��ȡֵ��Χ����{y}����2��д��y��ȡֵ��Χ��
(3)��֪x��y���㷽����![]() ����x��y��ȡֵ��Χ��
����x��y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com