
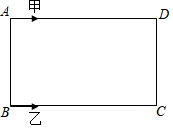
 如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.分析 (1)设经过t秒甲、乙两人第一次相遇,根据速度×时间=路程结合题意,即可得出关于t的一元一次方程,解之即可得出t值,进而即可得出2t值,由甲走过的路程结合各边长度即可得出第一次相遇的位置在DC边上;
(2)设从第一次相遇后经过m秒两人第二次相遇,根据速度×时间=路程结合题意,即可得出关于m的一元一次方程,解之即可得出m值,进而即可得出2m值,由甲走过的总路程结合各边长度即可得出第二次相遇的位置在BC边上.
解答 解:(1)设经过t秒甲、乙两人第一次相遇,
根据题意得:2t+3t=50+50+30,
解得:t=26,
∴2t=2×26=52.
∵50米<52米<80米,
∴他们相遇的位置在DC边上.
答:经过26秒甲、乙两人第一次相遇,相遇时的位置在DC边上.
(2)设从第一次相遇后经过m秒两人第二次相遇,
根据题意得:2m+3m=(50+30)×2,
解得:m=32,
∴2m=2×32=64,52+64=116(米).
∵80米<116米<130米,
∴他们相遇的位置在BC边上.
答:从第一次相遇后经过32秒两人第二次相遇,相遇时的位置在BC边上.
点评 本题考查了一元一次方程的应用,分析题干找准等量关系,正确列出一元一次方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com