
分析 可设直角三角形一直角边为x,则另一直角边为4$\sqrt{3}$-x,由面积为2作为相等关系列方程求得x的值,进而求得斜边的长.
解答 解:设直角三角形一直角边为x,则另一直角边为4$\sqrt{3}$-x,
根据题意得$\frac{1}{2}$x(4$\sqrt{3}$-x)=2,
解得:x=2$\sqrt{3}$-2$\sqrt{2}$或2$\sqrt{3}$+2$\sqrt{2}$,
∴另一直角边为2$\sqrt{3}$+2$\sqrt{2}$或2$\sqrt{3}$-2$\sqrt{2}$,
∴它的斜边长=$\sqrt{40}$=2$\sqrt{10}$.
点评 本题考查了勾股定理的运用,根据直角三角形的面积公式列出关于直角边的方程,解得直角边的长再根据勾股定理求斜边的长.熟练运用勾股定理和一元二次方程是解题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
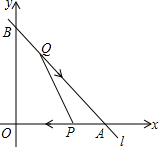 如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (-1,-3) | C. | (-3,1) | D. | (-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
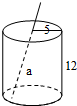 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分的长度x(罐壁厚度和小圆孔大小忽略不计)范围是( )
如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分的长度x(罐壁厚度和小圆孔大小忽略不计)范围是( )| A. | 12≤x≤13 | B. | 12≤x≤15 | C. | 5≤x≤12 | D. | 5≤x≤13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com