
【题目】如图,已知抛物线经过点A(﹣1,0),B(3,0),C(0,3)三点.
(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,请说明理由.
【答案】
(1)解:设抛物线的解析式为:y=a(x+1)(x﹣3),则:
a(0+1)(0﹣3)=3,a=﹣1;
∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.
(2)解:设直线BC的解析式为:y=kx+b,则有:
![]() ,
,
解得 ![]() ;
;
故直线BC的解析式:y=﹣x+3.
已知点M的横坐标为m,MN∥y,则M(m,﹣m+3)、N(m,﹣m2+2m+3);
∴故MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3).
(3)解:如图:
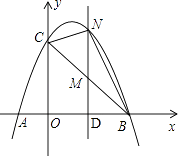
∵S△BNC=S△MNC+S△MNB= ![]() MN(OD+DB)=
MN(OD+DB)= ![]() MNOB,
MNOB,
∴S△BNC= ![]() (﹣m2+3m)3=﹣
(﹣m2+3m)3=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() (0<m<3);
(0<m<3);
∴当m= ![]() 时,△BNC的面积最大,最大值为
时,△BNC的面积最大,最大值为 ![]() .
.
【解析】(1)把ABC 坐标代入解析式即可;(2)竖直线段长等于上纵减下纵,须求BC的解析式;(3)斜三角形(没有竖直或水平边)的面积可通过做竖直线分割转化为竖直三角形(有一条边竖直边),即S△BNC=S△MNC+S△MNB,构建函数即可解决.


科目:初中数学 来源: 题型:
【题目】如图,将方格纸中的△ABC向上平移4个单位长度,然后向右平移6个单位长度,得到△A1B1C1.
(1)画出平移后的图形;
(2)线段AA1,BB1的位置关系是______;数量关系是________.
(3)如果每个方格的边长是1,那么△ABC的面积是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
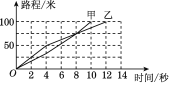
【题目】甲、乙两人进行比赛的路程与时间的关系如图所示.
(1)这是一场________米比赛;
(2)前一半赛程内________的速度较快,最终________赢得了比赛;
(3)两人第________秒在途中相遇,相遇时距终点________米;
(4)甲在前8秒的平均速度是多少?甲在整个赛程的平均速度是多少?乙在前8秒的平均速度是多少?乙在整个赛程的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y= ![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= ![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠ABC= ![]() ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则
,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则 ![]() 的值为( )
的值为( )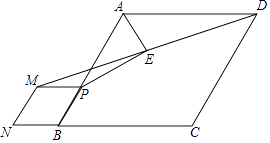
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转90°得到P′,连CP′,则线段CP′的最小值为 . 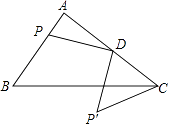
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑,2台B型打印机,一共需要花费5900元;如果购买2台A型电脑,2台B型打印机,一共需要花费9400元.
(1)求每台A型电脑和每台B型打印机的价格分别是多少元?
(2)如果学校购买A型电脑和B型打印机的预算费用不超过20000元,并且购买B型打印机的台数要比购买A型电脑的台数多1台,那么该学校至多能购买多少台B型打印机?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com