
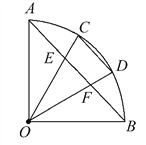
【题目】如图,∠AOB=90°,C,D是![]() 的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
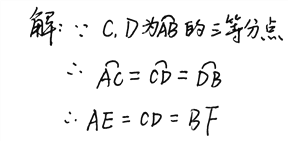
(1)错因: .
(2)纠错:____________________________________________________________
.
【答案】(1) AE,BF不是圆的弦,不能直接利用等弧对等弦(2)10
【解析】试题分析:先根据OA⊥OB可知∠AOB=90°,再由C、D为弧AB的三等分点可求出∠AOC的度数;由三角形内角和定理求出∠OCD的度数,根据三角形外角的性质得出∠OEF及∠OFE的度数,得OE=OF,CE=DF;根据三角形内角和定理即可得出∠AEO的度数;连接AC,BD,可得出CD=AE=BF,可得EF∥CD,所以EF<CD,即可得解.
解:∵在⊙O中,半径OA⊥OB,C、D为弧AB的三等分点,
∴∠AOC=![]() ∠AOB=
∠AOB=![]() ×90°=30°
×90°=30°
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠AOC=∠BOD=30°,
∴∠OEF=∠OAB+∠AOC=45°+30°=75°,同理∠OFE=75°,
∴OE=OF,
∴CE=DF;
连接AC,BD,

∵OC=OD,OE=OF,
∴EF∥CD,
∴EF<CD,
∵C,D是弧AB的三等分点,
∴AC=CD=BD,
∵∠AOD,
∴△ACO≌△DCO.
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD=![]() =75°,
=75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC.
故AC=AE,
同理,BF=BD.
又∵AC=CD=BD
∴CD=AE=BF.
故答案为:
OE=OF,CE=DF,CD=AE=BF.
点睛: 本题考查的是圆的综合题,涉及到等腰三角形的性质、全等三角形的判定定理等知识.解答本题的关键是求出△ACO≌△DCO,根据全等三角形对应边相等的性质得解.在同圆或等圆中,相等的圆心角或相等的弧所对的弦相等,不要认为所对的线段相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有( )

A. ②④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填![]() 或
或![]() );
);
(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

查看答案和解析>>
科目:初中数学 来源: 题型:
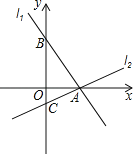
【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
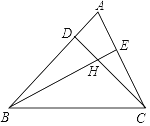
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),
(1)写出C点的坐标;
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动(当P点运动到A点时,两点都停止运动).设从出发起运动了x秒.
①请用含x的代数式分别表示P,Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E的坐标,若不存在,说明理由?
(3)在点P、Q运动过程中,过点Q作x轴的平行线DE,∠DQP与∠APQ的角平分线交于点M,则∠PMQ的大小会随点P、Q的运动而变化吗?如果不变化,请求出∠PMQ的度数;若发生变化,请说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com