练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．下列计算正确的是（　　）
    A．3x2-x2=3B．3a2+2a3=5a5C．5x3-x3=4x3D．-0.5ab+$\frac{1}{4}$ba=0

    分析 依据合并同类项法则进行判断即可．

    解答 解：A、3x2-x2=2x2，故A错误；
    B、3a2与2a3不是同类项，不能合并，故B错误；
    C、5x3-x3=4x3，故C正确；
    D、-0.5ab+$\frac{1}{4}$ba=$\frac{1}{4}$ba，故D错误．
    故选：C．

    点评 本题主要考查的是合并同类项，掌握同类项的定义以及合并同类项法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．如图，AD是△ABC的BC边上的中线，DE∥AB，若AB=5，则DE的长为2.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．【背景介绍】勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．
    【小试牛刀】把两个全等的直角三角形如图1放置，其三边长分别为a、b、c．显然，∠DAB=∠B=90°，AC⊥DE．请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：S梯形ABCD=$\frac{1}{2}$a（a+b），S△EBC=$\frac{1}{2}$b（a-b），S四边形AECD=$\frac{1}{2}$c2，则它们满足的关系式为$\frac{1}{2}$a（a+b）=$\frac{1}{2}$b（a-b）+$\frac{1}{2}$c2，经化简，可得到勾股定理．
    【知识运用】（1）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=24千米，BC=16千米，则两个村庄的距离为8$\sqrt{26}$千米（直接填空）．
    （2）在（1）的背景下，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP的距离．
    【知识迁移】借助上面的思考过程与几何模型，求代数式$\sqrt{{x}^{2}+9}$+$\sqrt{（16-x）^{2}+81}$的最小值（0＜x＜16）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

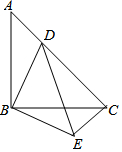    4．等腰Rt△ABC中，BA=BC，∠ABC=90°，将△ABD绕点B顺时针旋转90°后，得到△CBE．若AB=6，CD=2AD，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．先观察下列等式，再完成题后问题：21=2、22=4、23=8、24=16、25=32、26=64、27=128、28=256…
    （1）通过观察发现2n的个位数字是由4种数字组成；
    （2）用你所发现的规律写出22016的个位数字是6；
    （3）探究：32017的个位数字是3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

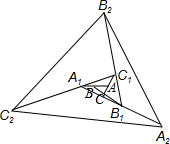    1．如图，△ABC面积为1，第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB、B1C=2BC，C1A=2CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1、C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=2B1C1，C2A1=2C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，经过2016次操作后△A2016B2016C2016的面积为72016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知直角三角形的两直角边的长分别为5和12，则斜边中线长为$\frac{13}{2}$，高线长为$\frac{60}{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

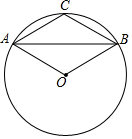    2．如图，已知AB为⊙O的弦长，且AB：AO=$\sqrt{3}$，点C为$\widehat{AB}$的中点，试猜想四边形AOBC的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

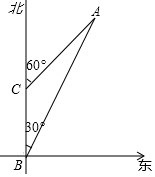    3．已知海岛A的周围6km的范围内有暗礁，一艘海轮在B处测得海岛A在北偏东30°的方向；向正北方向航行6km到达C处，又测得该岛在北偏东60°的方向，如果海轮不改变航向，继续向正北航行，有没有触礁的危险？

    查看答案和解析>>

    同步练习册答案