
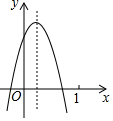
 二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )
二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据二次函数图象找出a、b、c之间的关系,再逐一分析四条结论的正误,由此即可得出结论.
解答 解:①∵抛物线开口向下,
∴a<0;
∵抛物线与y轴交点在y轴正半轴,
∴b>0,
∴ab<0,①正确;
②∵抛物线对称轴0<x=-$\frac{b}{2a}$<1,且当x=1时,y<0,
∴当x=-1时,y<0,
∴a-b+c<0,②正确;
③∵抛物线与x轴有两个不同的交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,③错误;
④根据二次函数图象可知:在对称轴左边y随x的增大而增大,在对称轴右边y随x的增大而减小,
∴④错误.
综上可知:正确的结论有①②.
故选C.
点评 本题考查了二次函数图象与系数的关系,根据二次函数的图象逐一分析四条结论的正误是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
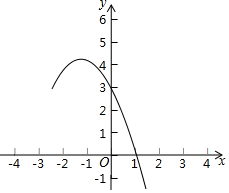 已知抛物线y=-x2+bx+c的部分图象如图所示.
已知抛物线y=-x2+bx+c的部分图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是菱形ABCD的边AB上一点,AB=4,∠DAB=60°,过E的直线EF∥AD交 AC、CD于点P、F,过P的直线GH∥AB交AD、BC于点G、H,设AE的长度为x,鱼形(阴影部分)的面积为y,则y关于x的函数解析式是y=$\frac{3\sqrt{3}}{4}$x2-4$\sqrt{3}$x+8$\sqrt{3}$.
如图,点E是菱形ABCD的边AB上一点,AB=4,∠DAB=60°,过E的直线EF∥AD交 AC、CD于点P、F,过P的直线GH∥AB交AD、BC于点G、H,设AE的长度为x,鱼形(阴影部分)的面积为y,则y关于x的函数解析式是y=$\frac{3\sqrt{3}}{4}$x2-4$\sqrt{3}$x+8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
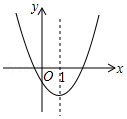 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$a元 | B. | $\frac{100}{81}$a元 | C. | a(1-10%)2元 | D. | a(1-10)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$=$\sqrt{3}$ | B. | $\sqrt{(-3)(-4)}$=$\sqrt{-3}$×$\sqrt{-4}$ | C. | $\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$ | D. | $\sqrt{42-32}$=$\sqrt{42}$-$\sqrt{32}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com