
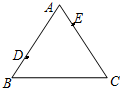
 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.
如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似. 分析 根据题意得出BD=2t,AE=t,得出AD=8-2t,分两种情况:①当$\frac{AD}{AB}=\frac{AE}{AC}$时,即$\frac{8-2t}{8}=\frac{t}{6}$,解方程即可;②当$\frac{AD}{AC}=\frac{AE}{AB}$时,即$\frac{8-2t}{6}=\frac{t}{8}$,解方程即可.
解答 解:根据题意得:BD=2t,AE=t,
∴AD=8-2t,
∵∠A=∠A,
∴分两种情况:
①当$\frac{AD}{AB}=\frac{AE}{AC}$时,
即$\frac{8-2t}{8}=\frac{t}{6}$,
解得:t=$\frac{12}{5}$;
②当$\frac{AD}{AC}=\frac{AE}{AB}$时,
即$\frac{8-2t}{6}=\frac{t}{8}$,
解得:t=$\frac{32}{11}$;
综上所述:当t=$\frac{12}{5}$或$\frac{32}{11}$时,△ADE与△ABC相似.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,并能进行推理计算是解决问题的关键;注意分类讨论.


科目:初中数学 来源: 题型:解答题
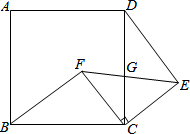 如图所示,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.
如图所示,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
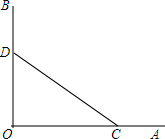 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 0道 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
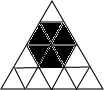 如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )
如图是某幼儿园活动室的一个正三角形活动区,老师让小朋友们向这个活动区扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形都是等可能的,扔1次沙包恰好击中阴影区域的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com