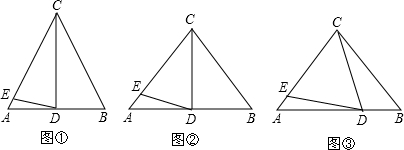
解:(1)∵AC=BC,CD为底边AB上的中线,
∴∠ECD=∠BCD=20°,CD⊥AB,
∴∠A=90°-∠ECD=70°.
又∵CD=CE,
∴∠CED=
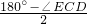
=80°,
∴∠ADE=∠CED-∠A=80°-70°=10°;
(2)∵AC=BC,CD为底边AB上的中线,
∴∠ECD=∠BCD=30°,CD⊥AB,
∴∠A=90°-∠ECD=60°.
又∵CD=CE,
∴∠CED=
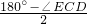
=75°,
∴∠ADE=∠CED-∠A=75°-60°=15°;
(3)∵∠BCD=20°时,∠ADE=10°;
∠BCD=30°时,∠ADE=15°;
∴∠BCD=2∠ADE.
(4)依然有∠BCD=2∠ADE.理由如下:
∵AC=BC,∴∠A=∠B.
∵∠BCD+∠B=∠ADE+∠CDE,
∴∠BCD+∠A=∠ADE+∠CDE.
∵CD=CE,∴∠CED=∠CDE,
∴∠BCD+∠A=∠ADE+∠CED,
∵∠CED=∠A+∠ADE,
∴∠BCD+∠A=∠ADE+∠A+∠ADE,
∴∠BCD=2∠ADE.
分析:(1)先根据等腰三角形三线合一的性质得出∠ECD=∠BCD=20°,根据等腰三角形等边对等角的性质及三角形内角和定理求出∠A=70°,∠CED=80°,再由三角形的一个外角等于和它不相邻的两个内角的和,得出∠ADE=∠CED-∠A;
(2)同(1),先根据等腰三角形三线合一的性质得出∠ECD=∠BCD=30°,根据等腰三角形等边对等角的性质及三角形内角和定理求出∠A=60°,∠CED=75°,再由三角形的一个外角等于和它不相邻的两个内角的和,即可得出∠ADE=∠CED-∠A;
(3)由(1)(2)中∠BCD与∠ADE的度数关系,容易发现∠BCD=2∠ADE;
(4)根据等腰三角形等边对等角的性质,三角形的外角性质及等式的性质即可证明∠BCD=2∠ADE依然成立.
点评:本题主要考查了等腰三角形的性质,三角形内角和定理,三角形的外角性质,综合性较强,难度中等.本题四问,循序渐进,体现了由特殊到一般的规律.

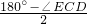 =80°,
=80°,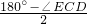 =75°,
=75°,

 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=