解:(1)解方程x
2-6x+5=0,得:x=1,x=5;
故m=1,n=5,
即A(1,0),B(0,5),
代入抛物线y=-x
2+bx+c中,得:

,
解得

;
即抛物线的解析式为:y=-x
2-4x+5;
当y=0时,-x
2-4x+5=0,
解得x=1,x=-5,故C(-5,0);
由于y=-x
2-4x+5=-(x+2)
2+9,
即D(-2,9);
设抛物线的对称轴与x轴的交点为E,则E(-2,0),
S
△BCD=S
梯形OEDB+S
△CDE-S
△COB=

(5+9)×2+

×3×9-

×5×5=15;
故抛物线与x轴的交点为(-2,0),
△BCD的面积为:15.
(2)由于C(-5,0),D(-2,9),则CD的中点Q(-

,

);
若直线l平分△BCD的面积,则直线l必经过Q、B两点,设直线l的解析式为:y=kx+5,则有:
-

k+5=

,k=

;
故直线l的解析式为:y=
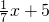
.
分析:(1)通过解方程可求得m、n的值,从而得到A、B的坐标,然后根据A、B的坐标即可确定抛物线的解析式,进而可求得抛物线的顶点坐标和对称轴方程;设抛物线的对称轴与x轴的交点为E,根据抛物线顶点D的坐标,可得到DE、OE的长,A、C的坐标易求得,即可得到OA、OC的值,可分别求出梯形OBDE、△CDE、△COB的面积,那么梯形OBDE、△CDE的面积和减去△COB的面积即为△BCD的面积.
(2)若直线l平分△BCD的面积,那么直线l必过CD的中点,可先根据C、D的坐标得到CD的中点坐标,然后结合点B的坐标,利用待定系数法求出直线l的解析式.
点评:此题主要考查了用待定系数法确定函数解析式的方法以及图形面积的求法,属于基础知识,需要熟练掌握.

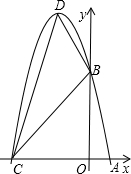 0,n)且此时抛物线与x轴的另一个交点为C,抛物线的顶点为D.
0,n)且此时抛物线与x轴的另一个交点为C,抛物线的顶点为D. ,
, ;
; (5+9)×2+
(5+9)×2+ ×3×9-
×3×9- ×5×5=15;
×5×5=15; ,
, );
); k+5=
k+5= ,k=
,k= ;
;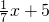 .
.
