
【题目】点 A(2,m),B(2,m-5)在平面直角坐标系中,点O为坐标原点.若△ABO是直角三角形,则m的值不可能是( )
A.4B.2C.1D.0
科目:初中数学 来源: 题型:
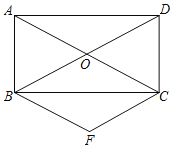
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过B点作BF∥AC,过C点作CF∥BD,BF与CF相交于点F.
(1)求证:四边形BFCO是菱形;
(2)连接OF、DF,若AB=2,tan∠OFD=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,若射线
,若射线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点![]() 为线段
为线段![]() 关于射线
关于射线![]() 的等腰点.
的等腰点.
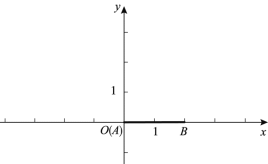
(1)如图, ![]() ,
,
①若![]() ,则线段
,则线段![]() 关于射线
关于射线![]() 的等腰点的坐标是_____;
的等腰点的坐标是_____;
②若![]() ,且线段
,且线段![]() 关于射线
关于射线![]() 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求![]() 的取值范围;
的取值范围;
(2) 若![]() ,且射线
,且射线![]() 上只存在一个线段
上只存在一个线段![]() 关于射线
关于射线![]() 的等腰点,则
的等腰点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
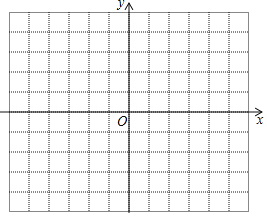
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏,现有三张形状大小完全相同的牌,正面分别标有数字![]() ,
,![]() ,
,![]() ,将三张牌背面朝上,洗匀后放在桌子上.
,将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为![]() 的倍数,则甲获胜;若抽取的数字和为
的倍数,则甲获胜;若抽取的数字和为![]() 的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.
的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
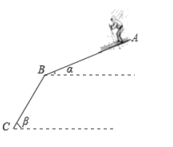
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为多少米.(结果保留整数)(参考数据sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中学生体质健康标准》规定学生体质健康等级标准: ![]() 分及以上为优秀;
分及以上为优秀; ![]() 分
分![]() 分为良好;
分为良好; ![]() 分
分![]() 分为及格;
分为及格;![]() 分以下为不及格.某校为了解学生的体质健康情况,从八年级学生中随机抽取了
分以下为不及格.某校为了解学生的体质健康情况,从八年级学生中随机抽取了![]() 的学生进行了体质测试,并将测试数据制成如下统计图.请根据相关信息解答下面的问题:
的学生进行了体质测试,并将测试数据制成如下统计图.请根据相关信息解答下面的问题:
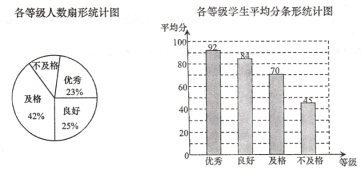
![]() 扇形统计图中,“不及格” 等级所在扇形圆心角的度数是多少?
扇形统计图中,“不及格” 等级所在扇形圆心角的度数是多少?
![]() 求参加本次测试学生的平均成绩;
求参加本次测试学生的平均成绩;
![]() 若参加本次测试“良好”及“良好”以上等级的学生共有
若参加本次测试“良好”及“良好”以上等级的学生共有![]() 人,请你估计全校八年级“不及格”等级的学生大约有多少人.
人,请你估计全校八年级“不及格”等级的学生大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意:B级满意;C级:基本满意:D级:不满意),并将调查结果绘制成如两幅不完整的统计图,请根据统计图中的信息解决下列问题:
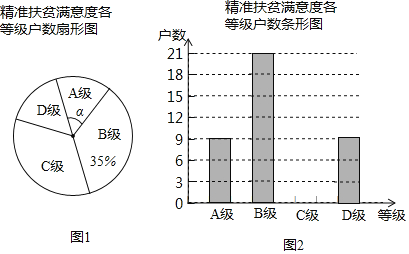
(1)本次抽样调查测试的建档立卡贫困户的总户数是 ;
(2)图①中,∠α的度数是 ,并把图②条形统计图补充完整;
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com