Question

从2、3、4、5这四个数中，任取两个数a和b（a≠b），构成函数y=ax-2和y=x+b，并使这两个函数图象的交点在直线x=2的右侧，则这样的有序数对（a，b）共有    个．

Answer 1

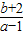
【答案】分析：首先令ax-2=x+b，解得x=，这两个函数图象的交点在直线x=2的右侧，可得＞2，即可求得符合要求的有序数对．
解答：解：令ax-2=x+b，解得x=．
∵这两个函数图象的交点在直线x=2右侧，即＞2，
整理得b＞2a-4．
∵a≠b，把a=2，3，4，5分别代入即可得相应的b的值，
∴有序数对为：（2，3），（2，4），（2，5），（3，4），（3，5），（4，5），
∴满足条件的有6对．
故答案为：6．
点评：本题考查根据交点坐标确定解析式字母系数的取值的知识．此题难度适中，注意分类讨论思想的运用．