
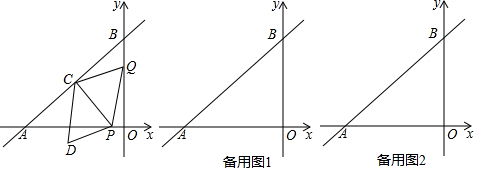
分析 (1)利用三角函数sin∠OAB=$\frac{PC}{AP}$=$\frac{OB}{AB}$,cos∠OAB=$\frac{OA}{AB}$=$\frac{AC}{AP}$,列出关系式即可解决问题.
(2)①当D在x轴上时,如图2中,由QC∥OA,得 $\frac{BQ}{OB}$=$\frac{BC}{AB}$,由此即可解决问题.
②当点D在AB上时,如图3中,由PQ∥AB,得$\frac{OQ}{OB}$=$\frac{OP}{OA}$,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.
(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO=$\frac{OB}{AB}$=$\frac{BN}{BQ}$,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
解答 解:(1)如图1中,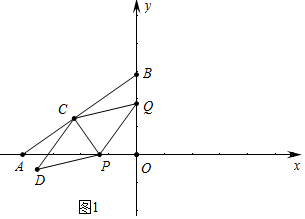
∵OA=3,OB=4,
∴AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△ACP中,PA=4-t,
∵sin∠OAB=$\frac{PC}{AP}$=$\frac{OB}{AB}$,
∴PC=$\frac{3}{5}$(4-t),
∵cos∠OAB=$\frac{OA}{AB}$=$\frac{AC}{AP}$,
∴AC=$\frac{4}{5}$(4-t).
(2)①当D在x轴上时,如图2中,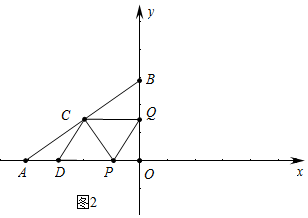
∵QC∥OA,
∴$\frac{BQ}{OB}$=$\frac{BC}{AB}$,
∴$\frac{2t}{3}$=$\frac{5-\frac{4}{5}(4-t)}{5}$,
解得t=$\frac{27}{38}$.
∴t=$\frac{27}{38}$s时,点D在x轴上,
②如图3中,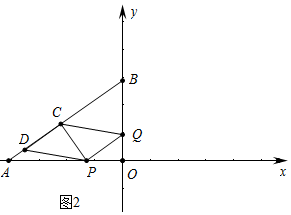
∵PQ∥AB,
∴$\frac{OQ}{OB}$=$\frac{OP}{OA}$,
∴$\frac{3-2t}{3}$=$\frac{t}{4}$,
∴t=$\frac{12}{11}$,
综上所述,当$\frac{27}{38}$<t<$\frac{12}{11}$时,点D落在△ABO内部(不包括边界).
(3)如图3中,作QN⊥BC于N,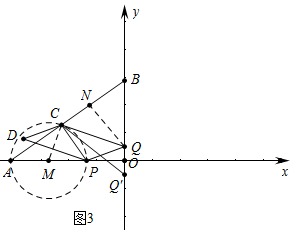
∵Q(0,3-2t),Q′(0,2t-3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,
∵cos∠ABO=$\frac{OB}{AB}$=$\frac{BN}{BQ}$,
∴$\frac{\frac{1}{2}[5-\frac{4}{5}(4-t)]}{2t}$=$\frac{3}{5}$,
解得t=$\frac{9}{8}$,
当CQ′是⊙M切线时,同法可得$\frac{\frac{1}{2}[5-\frac{4}{5}(4-t)]}{6-2t}$=$\frac{3}{5}$,
解得t=$\frac{27}{16}$,
∴t=$\frac{9}{8}$s或$\frac{27}{16}$时,过A,P,C三点的圆与△CQQ′三边中的一条边相切.
点评 本题考查圆的综合题、锐角三角函数、平行四边形的性质、等腰三角形的性质、切线的性质等知识,解题的关键是求得点D在特殊位置时的时间,学会利用方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
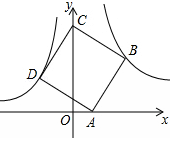 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C、D构成的四边形为正方形,求点A的坐标.
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C、D构成的四边形为正方形,求点A的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
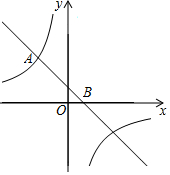 在平面直角坐标xOy中,直线y=kx+1(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为A(-2,3),与x轴交于点B.
在平面直角坐标xOy中,直线y=kx+1(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)的一个交点为A(-2,3),与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
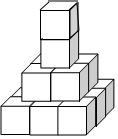 一个雕塑家利用15个棱长为1米的相同正方体,在公园空地设计了一个如图所示的几何体造型,需要把露出的表面分都涂上颜色,则需要涂颜色部分的面积为( )
一个雕塑家利用15个棱长为1米的相同正方体,在公园空地设计了一个如图所示的几何体造型,需要把露出的表面分都涂上颜色,则需要涂颜色部分的面积为( )| A. | 46米2 | B. | 37米2 | C. | 28米2 | D. | 25米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)
如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
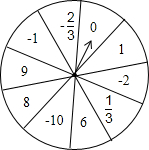 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com