
 ��֪����ͼƽ��ֱ������ϵxOy�У�C��x���ϣ��ı���OABCΪ���Σ���A������
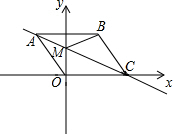
��֪����ͼƽ��ֱ������ϵxOy�У�C��x���ϣ��ı���OABCΪ���Σ���A���������� ��1�����ݹ��ɶ������ɵ�AO�ij����������ε����ʣ��ɵ�OC�ij������ݴ���ϵ�������ɵú�������ʽ��
��2���������ۣ��ٵ�0��t$��\frac{5}{2}$ʱ�������߶εĺͲ�ɵ�DM��BM�ij������������ε������ʽ���ɵô𰸣���0��t$��\frac{5}{2}$ʱ����������ĺͲ�ɵ�ME�ij������������������ʽ���ɵô𰸣�
��3������һ�κ��������ʣ��ɵú��������ֵ��
��� �⣺��1����ͼ1����AD��x����D�㣮 ��
��
�ɹ��ɶ�������
AO=$\sqrt{A{D}^{2}+O{D}^{2}}$=$\sqrt{��-3��^{2}+{4}^{2}}$=5��
�����εĶ��壬��OC=AO=AB=5��
C��5��0����
��AC�Ľ���ʽΪy=kx+b��ͼ���A��C�㣬
$\left\{\begin{array}{l}{5k+b=0}\\{-3k+b=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$��
ֱ��AC�Ľ���ʽy=-$\frac{1}{2}$x+$\frac{5}{2}$��
��2���ٵ�0��t$��\frac{5}{2}$ʱ����ͼ2�� ��
��
AC��y��Ľ������꣨0��$\frac{5}{2}$����
MD=OD-OM=4-$\frac{5}{2}$=$\frac{3}{2}$��
AP=2t��PB=5-2t��
S=$\frac{1}{2}$PB•MD����S=$\frac{1}{2}$��$\frac{3}{2}$����5-2t����
����S=$\frac{15}{4}$-$\frac{3}{2}$t��
�ڵ�$\frac{5}{2}$��t��5ʱ����ME��BC��E�㣬��ͼ3�� ��
��
S��ABC=$\frac{1}{2}$SAOCB=$\frac{1}{2}$OC•OD=10��
S��ABC=S��ABM+S��BCM=$\frac{1}{2}$��5��$\frac{3}{2}$+$\frac{1}{2}$��5ME=10��
���ME=$\frac{5}{2}$��
S=$\frac{1}{2}$PB•ME����S=$\frac{1}{2}$��$\frac{5}{2}$��2t-5����
����S=$\frac{5}{2}$t-$\frac{25}{4}$��
����������S=$\left\{\begin{array}{l}{-\frac{3}{2}t+\frac{15}{4}��0��t��\frac{5}{2}��}\\{\frac{5}{2}t-\frac{25}{4}��\frac{5}{2}��t��5��}\end{array}\right.$��
��3���ٵ�0��t��$\frac{5}{2}$ʱ��S��t���������С����t=0ʱ��S���=$\frac{15}{4}$��
�ڵ�$\frac{5}{2}$��t��5ʱ��s��t�����������t=5ʱ��S���=$\frac{25}{4}$��
������������t=5ʱ��S���=$\frac{25}{4}$��
���� ���⿼����һ�κ����ۺ��⣬��1���������ε����ʵó�OC�ij��������ô���ϵ�����ó���������ʽ����2�����������ε������ʽ�ó���������ʽ�����������ǽ���ؼ�����3�����ú������������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬AB=10���Ե�CΪԲ�ģ�CAΪ�뾶��Բ��AB���ڵ�D��$sinB=\frac{3}{5}$��
��ͼ����Rt��ABC�У���ACB=90�㣬AB=10���Ե�CΪԲ�ģ�CAΪ�뾶��Բ��AB���ڵ�D��$sinB=\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����C��B��E��ͬһ��ֱ���ϣ�AC��BC��BD��DE��AC=BD=6��AB=10����A=��DBE
��ͼ����C��B��E��ͬһ��ֱ���ϣ�AC��BC��BD��DE��AC=BD=6��AB=10����A=��DBE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
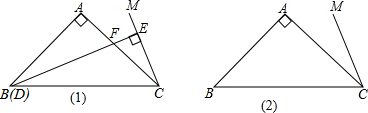
 ��ͼ����ACB�͡�ADE���ǵ���ֱ�������Σ���BAC=��DAE=90�㣬��C��D��E������ͬһֱ���ϣ�����BD�����BDE=90�ȣ�
��ͼ����ACB�͡�ADE���ǵ���ֱ�������Σ���BAC=��DAE=90�㣬��C��D��E������ͬһֱ���ϣ�����BD�����BDE=90�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com