
分析 (1)首先去分母,然后去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组组的解集.
解答 解:(1)去分母5(3y-1)-2y<10y+10
去括号15y-5-2y<10y+10
移项3y<15
得y<5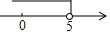 ;
;
(2)$\left\{\begin{array}{l}{-2x+1>-11…①}\\{\frac{3x+1}{2}-1≥x…②}\end{array}\right.$,
解①得x<6,
解②得x≥1,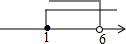 .
.
不等式组的解集为1≤x<6.
点评 本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.


科目:初中数学 来源: 题型:解答题
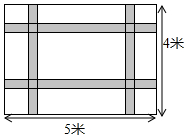 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
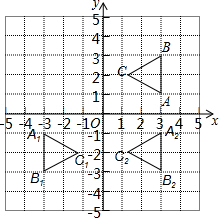 如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
如图,平面直角坐标系中,△ABC为等边三角形,其中点A,B,C的坐标分别为(3,1),(3,3),(3-$\sqrt{3}$,2),现以原点为对称中心作△ABC的中心对称图形,得△A1B1C1,再以y轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
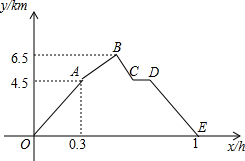 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发x h后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | -1 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com