
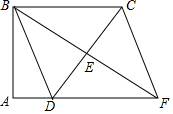
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.分析 (1)根据DE=EC,AF∥BC,得出内错角相等,证明△BCE≌△FDE,可判断BC∥DF且BC=DF,从而得出四边形BCDF为平行四边形;
(2)当BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,求出CG 即可解决问题.
解答 解:(1)∵AF∥BC,
∴∠DCB=∠CDF,∠FBC=∠BFD,
又DE=EC,
∴△BCE≌△FDE;
∴DF=BC,
又∵DF∥BC,
∴四边形BCDF为平行四边形;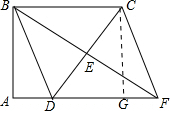
(2)当BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,
在Rt△CDG中,DG=BC-AD=2,CG=$\sqrt{C{D}^{2}-D{G}^{2}}$=$\sqrt{5}$,
∴S平行四边形BDFC=BC•CG=3$\sqrt{5}$.
点评 本题考查了直角梯形的性质,全等三角形的判定与性质,平行四边形、菱形的判定与性质.关键是利用梯形上下两底的平行关系及中点,证明两个三角形全等.


科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
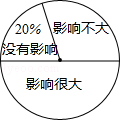 近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
近年来,学校对“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题密切关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数(人) | 40 | 60 | m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
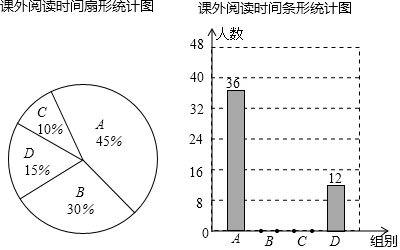
| 组别 | 课外阅读t(单位:时) |
| A | X<2 |
| B | 2≤x<3 |
| C | 3≤x<4 |
| D | x≥4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com