
【题目】如图,![]() 与
与![]() 中,
中,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() .
.
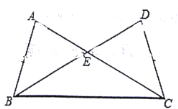
(1)求证:![]() ;
;
(2)当![]() ,求
,求![]() 的度数?
的度数?
【答案】(1)见解析;(2)25°.
【解析】
(1)根据条件直接可证明△ABE≌△DCE,然后在通过∠ABC=∠DBC,证明△ABC和△DCB全等即可;(2)根据三角形全等得出EB=EC,推出∠EBC=∠ECB,根据三角形的外角性质得出∠AEB=2∠EBC,代入求出即可.
(1)证明:在△ABE和△DCE中,
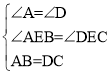
∴△ABE≌△DCE(AAS),
∴BE=EC,∠ABE=∠DCE,
∴∠EBC=∠ECB,
∵∠EBC+∠ABE=∠ECB+∠DCE,
∴∠ABC=∠DBC,
在△ABC和△DCB中,
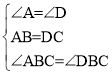
∴△ABC≌△DCB(ASA);
(2)∵∠AEB=50°,
∴∠EBC+∠ECB=50°,
∵∠EBC=∠ECB,
∴∠EBC=25°.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
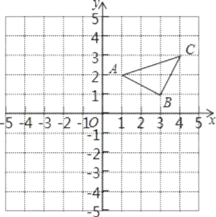
【题目】已知:如图所示.
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.

供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB、AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF=![]() ,④S△CGE:S△CAB=1:4.其中正确的是( )
,④S△CGE:S△CAB=1:4.其中正确的是( )
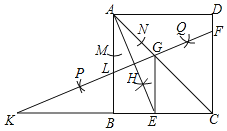
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
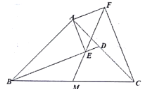
【题目】如图所示,![]() 是等腰直角三角形,其中
是等腰直角三角形,其中![]() ,
,![]() 是
是![]() 边上的一点,连接
边上的一点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于
于![]() 点.若四边形
点.若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个各数位上的数字均不为![]() 的三位自然数
的三位自然数![]() ,将它各个数位上的数字平方后再取其个位,得到三个新的数字;再将这三个新数字重新组合成三位数
,将它各个数位上的数字平方后再取其个位,得到三个新的数字;再将这三个新数字重新组合成三位数![]() ,当
,当![]() 的值最小时,称此时的
的值最小时,称此时的![]() 为自然数
为自然数![]() 的“理想数”,并规定:
的“理想数”,并规定:![]() ,例如
,例如![]() ,各数字平方后取个位分别为
,各数字平方后取个位分别为![]() ,
,![]() ,
,![]() ,再重新组合为
,再重新组合为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,因为
,因为![]() 最小,所以
最小,所以![]() 是原三位数
是原三位数![]() 的理想数,此时
的理想数,此时![]()
(1)求:![]() .
.
(2)若有三位自然数![]() ,满足有两个数位上的数字相同且不等于
,满足有两个数位上的数字相同且不等于![]() ,另一个数位上的数字为
,另一个数位上的数字为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面看上去无差别的卡片A,B,C,D,每张卡片的正面标有字母a,b,c表示三条线段(如图),把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

(1)用树状图或者列表表示所有可能出现的结果;
(2)求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
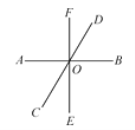
【题目】如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,![]() ,求∠DOF和∠FOC的度数.
,求∠DOF和∠FOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两地相距300千米,甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留1小时后,速度不变,按原路返回.设两车行驶的时间是x小时,离开A地的距离是y千米,如图是y与x的函数图象.
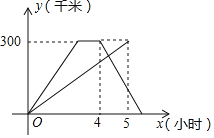
(1)甲车的速度是 ,乙车的速度是 ;
(2)甲车在返程途中,两车相距20千米时,求乙车行驶的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com