
 的最小值。
的最小值。科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点C是线段BD的中点,在BD的同侧分别等边△ABC和等边△CDE,点F是DE的中点,BF分别交AC、CE于G、H两点.
如图,点C是线段BD的中点,在BD的同侧分别等边△ABC和等边△CDE,点F是DE的中点,BF分别交AC、CE于G、H两点.查看答案和解析>>
科目:初中数学 来源: 题型:
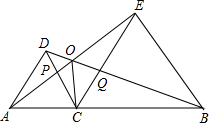
 如图,点C为线段AB上任意一点(不与A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.
如图,点C为线段AB上任意一点(不与A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和等腰△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接PC.查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第19~26期 总第175~182期 华师大版 题型:044
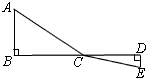
如图,点C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,垂足分别为B、D,连结AC、EC.已知AB=5,DE=1,BD=8,设CD=x.

(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小?
(3)根据(2)中规律和结论,请构图求出代数式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com