
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
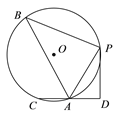
【答案】2
【解析】分析: 连接PC PB PA,过P做BA垂线于H点,根据PB=PC,再由全等三角形的判定定理可得出△PBH≌△PCD,Rt△PHA≌Rt△PDA,根据AC=AD=1即可得出结论.
详解: 连接PC PB PA,过P做BA垂线于H点,
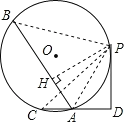
∵PD⊥CD, PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,
,
∴AP=![]() ,AD=1,
,AD=1,
∵AC=AD,
∴CD=2.
在△PBH与△PCD中,
∠B=∠C
PB=PC
∠BPH=∠DPC,
∴△PBH≌△PCD(ASA),
∴BH=CD=2,PH=PD=![]() ,
,
∴AH= ,
,
∴△PAB的面积为AB×PH×![]() =(2+1)×
=(2+1)×![]() ×
×![]() =2,
=2,
故答案为:2.
点睛:
本题考查的是圆周角定理及全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解答此题的关键.


科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和![]() 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同.
![]() 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率;
![]() 如果平均每人每月可投递快递
如果平均每人每月可投递快递![]() 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C,D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨:从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨,现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求y与x的函数关系式.
(3)怎样调运才能使总运费最少?并求最少运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
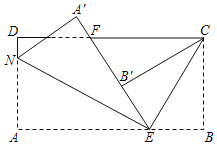
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com