
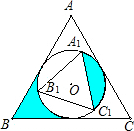
 如图,已知,正△A1B1C1的外接圆⊙O内切于正△ABC,若△ABC的面积是4
如图,已知,正△A1B1C1的外接圆⊙O内切于正△ABC,若△ABC的面积是4 ,则阴影部分的面积是
,则阴影部分的面积是

 +π
+π a,根据等边三角形的性质求出OD、AD,根据三角形的面积公式和勾股定理求出BC、AD、OD,根据勾股定理和含30°角的直角三角形的性质求出DE、EC1,进一步求出A1C1及边上的高,根据三角形的面积公式求出△A1B1C1的面积,根据式子
a,根据等边三角形的性质求出OD、AD,根据三角形的面积公式和勾股定理求出BC、AD、OD,根据勾股定理和含30°角的直角三角形的性质求出DE、EC1,进一步求出A1C1及边上的高,根据三角形的面积公式求出△A1B1C1的面积,根据式子 ×(△ABC的面积-△A1B1C1的面积),代入求出即可.
×(△ABC的面积-△A1B1C1的面积),代入求出即可.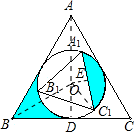 解:解法(1)
解:解法(1) a,
a, a,
a, ,
, ×a×
×a× a=4
a=4 ,
, ×60°=30°,
×60°=30°, BO,
BO, ,
, ,
, OC1=
OC1= ,
, =
= ,
, ×2×
×2× =
= ,
, ×(△ABC的面积-△A1B1C1的面积)=
×(△ABC的面积-△A1B1C1的面积)= ×(4
×(4 -
- )=
)= ,
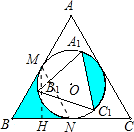
,
 ,
, BN×MH=
BN×MH= ×2×
×2× =
= .
.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数y=
如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•资阳)如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为( )
(2010•资阳)如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•建阳市模拟)如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数y=
(2012•建阳市模拟)如图,已知△OP1A1、△A1P2A2、△A2P3A3、…均为等腰直角三角形,直角顶点P1、P2、P3、…在函数y=| 4 |
| x |
| 2011 |
| 2012 |
| 2011 |
| 2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com