
分析 (1)可根据“改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元”,列出方程组求出答案;
(2)要根据“国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元”来列出不等式组,判断出不同的改造方案.
解答 解:(1)设改扩建一所A类和一所B类学校所需资金分别为x万元和y万元
由题意得$\left\{\begin{array}{l}{2x+3y=7800}\\{3x+y=5400}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1200}\\{y=1800}\end{array}\right.$,
答:改扩建一所A类学校和一所B类学校所需资金分别为1200万元和1800万元.
(2)设今年改扩建A类学校a所,则改扩建B类学校(10-a)所,
由题意得:$\left\{\begin{array}{l}{(1200-300)a+(1800-500)(10-a)≤11800}\\{300a+500(10-a)≥4000}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a≥3}\\{a≤5}\end{array}\right.$,
∴3≤a≤5,
∵x取整数,
∴x=3,4,5.
即共有3种方案:
方案一:改扩建A类学校3所,B类学校7所;
方案二:改扩建A类学校4所,B类学校6所;
方案三:改扩建A类学校5所,B类学校5所.
点评 本题考查了一元一次不等式组的应用,二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的数量关系.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-y)2=x2-y2 | B. | |$\sqrt{3}$-2|=2-$\sqrt{3}$ | C. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{5}$ | D. | -(-a+1)=a+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
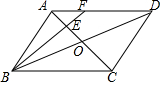 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )| A. | ①②③④ | B. | ①④ | C. | ②③④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com