
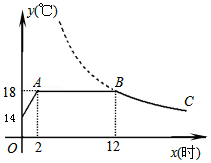
 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=$\frac{k}{x}$的一部分.请根据图中信息解答下列问题:分析 (1)观察图象即可解决问题;
(2)把B点坐标代入反比例函数解析式,即可解决问题;
(3)求出y=16时的两个时间,求出差即可解决问题;
解答 解:(1)12-2=10,
故恒温系统在这天保持大棚内温度18℃的时间有10个小时.
(2)把B(12,18)代入y=$\frac{k}{x}$中,k=216.
(3)设开始部分的函数解析式为y=kx+b,则有$\left\{\begin{array}{l}{2k+b=18}\\{b=14}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=2}\\{b=14}\end{array}\right.$,
∴y=2x+14,
当y=16时,x=1,
对于y=$\frac{216}{x}$,y=16时,x=13.5,
13.5-1=12.5,
答:这天该蔬菜能够快速生长的时间为12.5h.
点评 本题考查一次函数的应用、反比例函数的应用等知识,解题的关键是读懂图象信息,熟练应用待定系数法解决问题.


科目:初中数学 来源: 题型:填空题
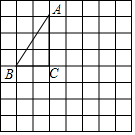 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
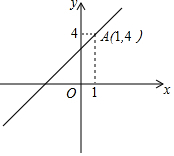 已知,一次函数y=kx+3的图象经过点A(1,4).
已知,一次函数y=kx+3的图象经过点A(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
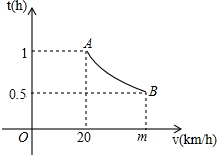 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$,其图象为如图所示的一段曲线且端点为A(20,1)和B(m,0.5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
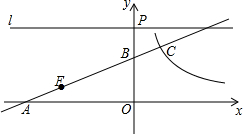 已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题:
已知:如图,直线y=$\frac{1}{2}$x+b与x轴负半轴交于点A,与y轴正半轴交于点B,线段OA的长是方程x2-7x-8=0的一个根,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com