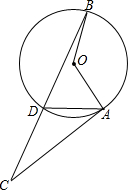练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，点A，D，B为⊙O上的三点，∠AOB=120°，且过A的直线交BD延长线于点C，连接AD，且AD=CD，则∠C的度数为30°．

    分析 由等腰三角形的性质得出∠C=∠DAC，由圆周角定理求出∠ADB=$\frac{1}{2}$∠AOB=60°，再由三角形的外角性质即可得出结果．

    解答 解：∵AD=CD，
    ∴∠C=∠DAC，
    ∵∠ADB=$\frac{1}{2}$∠AOB=60°，
    ∴∠C=∠DAC=$\frac{1}{2}$∠ADB=30°；
    故答案为：30°．

    点评 本题考查了圆周角定理、等腰三角形的性质、三角形的外角性质．此题难度适中，熟练掌握圆周角定理和等腰三角形的性质是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．某市需要铺设一条长660米的管道，为了尽量减少施工对城市交通造成的影响，实际施工时，每天铺设管道的长度比原计划增加10%，结果提前6天完成．求实际每天铺设管道的长度与实际施工天数．小宇同学根据题意列出方程：$\frac{660}{x}-\frac{660}{x（1+10%）}=6$．则方程中未知数x所表示的量是（　　）
    A．实际每天铺设管道的长度B．实际施工的天数
    C．原计划每天铺设管道的长度D．原计划施工的天数

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C，且OA=OC，则下列结论：①abc＜0；②$\frac{{b}^{2}-4ac}{4a}＞0$；③ac-b+1=0；④OA•OB=-$\frac{c}{a}$．其中正确结论的序号是①③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列四组数分别是三条线段的长度，能构成三角形的是（　　）
    A．1，1，2B．1，3，4C．2，3，6D．4，5，8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：（-π）0+2tan45°-（$\frac{1}{3}$）-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

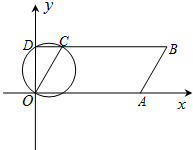    16．如图，在平面直角坐标系中，以OC为直径的圆交y轴于点D，∠DOC=30°，OC=2．延长DC至点B，使得CB=4DC，过B点作BA∥OC交x轴于A点．
    （1）请求出BC的长度；
    （2）若P点与B点是关于直线AC的对称点，试求出点P的坐标；
    （3）若点M、N分别为CB、AB上的动点，P点与B点是关于直线MN的对称点，过点P作x轴的平行线，与AC、OC分别交于点E、F．若PE﹕PF=1：3，点P的横坐标为m．请求出点P的纵坐标，并直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，点A、B、C、D在同一直线上，BE∥DF，∠A=∠F，AB=FD．求证：AE=FC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽BEF；④S△BEF=$\frac{72}{5}$．在以上4个结论中，其中一定成立的是①②④（把所有正确结论的序号都填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．化简求值：$\frac{x}{{x}^{2}-1}$$÷\frac{{x}^{2}+x}{{x}^{2}+2x+1}$-$\frac{{x}^{2}}{x-1}$．

    查看答案和解析>>

    同步练习册答案